Механический генератор случайных чисел

В школе я увлекался настольными играми, в основном варгеймами. Придумывал правила, изготавливал поля, юниты и проводил с друзьями увлекательные баталии. Однако вскоре для моделирования различных игровых ситуаций перестало хватать стандартного игрового кубика, с помощью которого можно получать вероятности, кратные одной шестой. Поиск решения породил пару интересных математических задач, связанных с теорией вероятности.

Итак, допустим, имея игровой кубик, нам нужно получить событие, вероятность которого равна 1/5. Для этого рассмотрим такой процесс: кубик бросается до тех пор, пока на нём не выпадет число, не равное шести. Очевидно, что в конечном итоге вероятности получить одно из чисел от 1 до 5 будут равны 1/5. Найдём, какое в среднем количество бросков потребуется сделать, чтобы серия шестёрок завершилась другим числом (иными словами, математическое ожидание данное величины).

С вероятностью  потребуется сделать всего один бросок. Серия будет иметь длину в два броска с вероятность . В три – с вероятностью  и т.д. Найдём сумму:

Её несложно будет вычислить, представив в следующем виде:

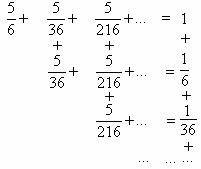
Таким образом, искомая сумма будет равна сумме геометрической прогрессии с первым членом 1, и знаменателем 1/6.

.

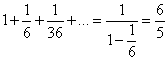В итоге математическое ожидание количества бросков для получения результата равно 1,2.

Рассмотрим теперь, как получать события с вероятностями, меньшими 1/6. К примеру, как сделать механический генератор случайных чисел от 1 до 36. Для этого можно обратиться к помощи систем счисления. Тридцать шесть чисел от 0 до 35, записанные в шестеричной системе счисления будут двузначными, от 00 до 55. Таким образом, если взять два кубика, таких, чтобы по виду можно было определить, какой из них первый, а какой второй, и нанести им на грани цифры от 0 до 5, каждый бросок будет нам давать случайное число от 0 до 35, записанное в шестеричной системе. Чтобы исключить необходимость оперирования недесятичной системой и получать числа из диапазона 1..36, нанесём на один кубик числа 1, 2, 3, 4, 5, 6, а на другой – 0, 6, 12, 18, 24, 30.

Если же нам необходимы случайные числа от 1 до 18, то на первый кубик наносятся числа от 1 до 6, а на второй: 0, 0, 6, 6, 12, 12.

Объединив оба подхода, можно с помощью трёх кубиков получать события с вероятностями, кратными 1/100. Для этого возьмём 3 кубика, два, такие, как в системе, дающей числа от 1 до 36, а на грани третьего нанесём числа 0, 0, 36, 36, 72, 72. С её помощью будем получать числа от 1 до 108. Если теперь при выпадении значений от 101 до 108 бросать кубики снова, и останавливаться только в случае получения числа от 1 до 100, мы сможем замоделировать любую вероятность, кратную целому числу процентов. Даже для самых сложных правил настольных игр этого должно хватить.

По мотивам этой темы можно составить задачу. Имеется арифметическая прогрессия a1, a2, a3, … с разностью d, и геометрическая прогрессия b1, b2, b3, … со знаменателем -1<q<1. Требуется найти сумму a1b1+a2b2+a3b3+…. Разобравшись с тем, как мы находили математическое ожидание количества бросков, её решить будет несложно.

Поздравляю Вас с наступающим Новы Годом и желаю, чтобы все возможные расклады были для Вас удачными!