- Интересные свойства чисел (6)→
- Математические сайты (7)→
- Логические игры (8)→
- О числе пи (5)→
- Форма расчёта налогов
- Превращаем цифры в забавных животных
- Как Ричард Фейнман победил японского вычислителя
- Как выводятся тригонометрические формулы
- Магические квадраты
- Цепные дроби
- Проблема 3x+1
- Вычислительные приёмы
- О сумме цифр, обобщённом признаке делимости и одной нерешённой задаче
- Генетический бассейн
- Совершенные, дружественные, и компанейские числа
- Механический генератор случайных чисел
- Что делать, если забыл математическую формулу? Вывести!
- Как писать самоописывающие тексты
- Нелинейная модель линейной тактики
- С Новым годом!!!
Все знают, что если сумма цифр числа делится на 9, то и сумма его цифр делится на 9. А для определения, делится ли число на 11, нужно сложить его цифры, стоящие на чётных местах и отнять сумму цифр, стоящих на нечётных местах. Если результат будет делиться на 11, то и само число также будет делиться на 11.
Возникает вопрос: почему существуют признаки делимости? Иными словами, почему для ответа на вопрос, делится ли число m на число n, достаточно не выполнять деление, а провести некоторые операции с цифрами числа m? И как вывести признак делимости на произвольное n. К ответу на этот вопрос мы придём, решая одну, казалось бы, пустяковую задачку.
Задача
Возьмём какое-нибудь натуральное число, скажем, 17. Сумма его цифр равна 8. Если 17 умножить на 2, получим 34 и сумма цифр этого числа окажется равной 7. А у произведения 17*3=51 сумма цифр равна 6. Вопрос: на какое натуральное число нужно умножить 17, чтобы сумма цифр произведения была наименьшей?
Решение
Понятно, что сумма цифр, равная 1 будет только у степеней десятки, которые кратны лишь произведениям степеней двойки и пятёрки. Поэтому попробуем найти кратное 17-ти число вида 100…01 с суммой цифр, равной двум.
17*X=100…01
Чтобы последней цифрой произведения была единица, последней цифрой неизвестного множителя должна быть тройка. Далее, т.к. 17*3=51, а предпоследняя цифра произведения равна 0, то предпоследней цифрой неизвестного множителя должна быть пятёрка.
17*53=901
Третьей с конца цифрой множителя снова должна быть тройка (чтобы произведение оканчивалось на ..001)
17*353=6001.
Далее находим, последовательно:
17*2353=40001
17*82353=1400001
17*882353=15000001
17*5882353=100000001 (!)
Весь этот процесс представлен на анимированной гиф-иллюстрации

Итак, среди чисел, кратных 17-ти наименьшая сумма цифр, равная 2, будет у числа 100000001=17*5882353.
Ответ: число 17 нужно умножить на 5882353, и тогда сумма цифр произведения будет равна 2.
Возникает вторая задача: а что было бы, если бы потребовалось найти кратное с минимальной суммой цифр для какого-нибудь другого числа? Почти сразу приходят на ум числа 3 и 9, кратные которых, вследствие соответствующих признаков делимости, не могут иметь суммы цифр, меньшие, чем 3 или 9, соответственно. Но оказывается, что и многие другие числа не имеют кратных вида 100…01.
К примеру, попробуем провести операции, аналогичные проведённым с числом 17, для числа 41.
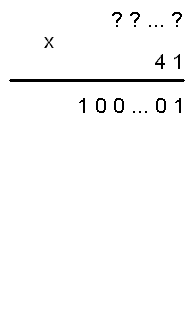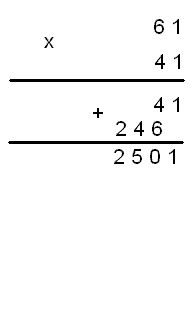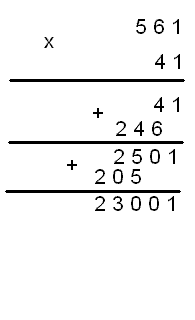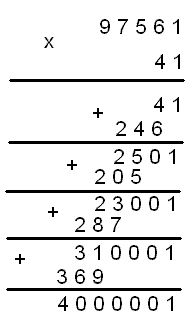
Если существует такой множитель Х, что 41*Х=100…01, то последняя цифра числа Х равна 1.
41*1=41.
Далее, предпоследняя цифра числа Х должна быть равна 6
41*61=2501
Далее получаем, последовательно:
41*561=23001
41*7561=310001
41*97561=4000001
И тут мы обнаруживаем, что зациклились: далее неизвестный множитель будет продолжать обрастать цифрами 6, 5, 7 и 9, а сумма цифр кратного, равная 2, достигнута не будет.
Итак, какова же минимальная сумма цифр у числа, кратного 41-му?
Вот тут мы и приходим к проблеме построения обобщённого признака делимости. Почему же для ответа на вопрос, делится ли число m на число n, достаточно не выполнять деление, а провести некоторые операции с цифрами числа m?
Как известно, если число m имеет k цифр, то его можно представить в виде суммы произведений его цифр на соответствующие степени десятки:
![]()
Далее, известно, что сумма остатков равна остатку суммы, а произведение остатков равно остатку произведения. Тогда, если j-я степень десятки даёт остаток ![]() при делении на n, то остаток числа m при делении на n будет равен остатку от деления на n выражения
при делении на n, то остаток числа m при делении на n будет равен остатку от деления на n выражения ![]()
Этот обобщённый признак делимости называется признаком Паскаля.
Докажем теперь с помощью этого признака делимости, что не существует числа вида 100…01, которое делится на 41. Вычислим остатки от деления на 41 степеней десятки:
j |
|
Остаток от деления на 41 |
0 |
1 |
1 |
1 |
10 |
10 |
2 |
100 |
18 |
3 |
1000 |
16 |
4 |
10000 |
37 |
5 |
100000 |
1 |
6 |
1000000 |
10 |
… |
… |
… |
Заметим, что удобнее находить искомые остатки не непосредственно делением степени числа 10 на 41, а делением на 41 предыдущего остатка, умноженного на 10. И, поскольку каждый следующий остаток однозначно зависит от предыдущего, то, получив на шестом шаге единицу, мы видим, что последовательность зациклилась.
Следовательно, признак делимости на 41 можно сформулировать следующим образом:
Чтобы проверить, делится ли число на 41, его следует справа налево разбить на грани по 5 цифр в каждой. Затем в каждой грани первую справа цифру умножить на 1, вторую цифру умножить на 10, третью – на 18, четвёртую – на 16, пятую – на 37 и все полученные произведения сложить. Если результат будет делиться на 41, тогда и только тогда само число будет делиться на 41.
Таким способом можно получать признаки делимости на любые числа.
Возвращаясь к задаче о минимальной сумме цифр кратного, мы убеждаемся, что число с двумя единицами и остальными цифрами – нулями на 41 разделиться не может.
Перебирая не более чем 5-ти значные числа с суммами цифр 3 и 4 (это можно сделать как на компьютере, так и вручную) оказывается, что среди чисел, кратных 41-му минимальную сумму цифр, равную 5, будет иметь само число 41.
Другое интересное число, 31, замечательно тем, что, хотя на 3 не делится, никакое из его кратных не может иметь сумму цифр, меньше трёх. В первый раз минимум достигается в числе 31*322581=10000011
Собственно, вот и та самая нерешённая задача, о которой сказано в заголовке. Исследование поведения последовательности минимальных сумм цифр кратных чисел (обозначим эту функцию minmds(n) – minimal multiples’ digits sum) представляет собой открытую проблему. Мы с моим учителем, а ныне и коллегой, Сергеем Тихоновичем Кузнецовым, оптимизировали алгоритм поиска и сейчас имеются данные по 56000 чисел.
По этим данным можно построить следующую таблицу:
k |
Количество чисел в диапазоне 1-56000 с minmds(n)=k |
Минимальное n, такое, что minmds(n)=k |
1 |
65 |
1 |
2 |
15544 |
7 |
3 |
26521 |
3 |
4 |
3889 |
79 |
5 |
939 |
41 |
6 |
2485 |
33 |
7 |
143 |
239 |
8 |
23 |
2629 |
9 |
5581 |
9 |
10 |
21 |
2981 |
11 |
2 |
21649 |
12 |
89 |
813 |
13 |
0 |
? |
14 |
1 |
51139 |
15 |
4 |
13947 |
16 |
0 |
? |
17 |
0 |
? |
18 |
632 |
99 |
… |
0 |
? |
27 |
56 |
999 |
… |
0 |
? |
36 |
5 |
9999 |
Сразу возникает очевидный и интересный вопрос: для какого числа x minmds(x)=13? (И существует ли такое число вообще?) И как по числу определить его minmds, по возможности наименее прибегая к перебору? Существует ли не кратное трём число с minmds, равным 9? (На этот можно ответить при внимательном изучении прилагаемого файла ;)
Таких вопросов можно набрать множество, и решать их будет одинаково интересно как математику-профессионалу, так и учащемуся при написании работы в Малой академии наук.
Задайте вопрос на блоге о математике
