Нелинейная модель линейной тактики

Каждый, кто играл в такие игры, как "Казаки", "Геттисберг", или смотрел исторические фильмы наподобие "Патриота", представляет, как в основном выглядели пехотные сражения с конца XVII до середины XIX века. Подразделения противоборствующих сторон выстраивались в тонкие линии друг напротив друга и давали по противнику залп за залпом.
Управляя компьютерными армиями задумываешься, что скорее развивать: скорострельность или точность, какое численное превосходство нужно создать для прорыва. Попробуем ответить на эти вопросы, построив математическую модель перестрелки двух линий пехоты.
Итак, пусть вначале имеется a солдат Красных и b солдат Синих. Известно, что в среднем на 1 выстрел красных приходится p убитых солдат синих и на 1 выстрел синих приходится q убитых солдат красных. Примем, что залпы производятся с одинаковой частотой и одновременно, т.е. все солдаты, прежде чем быть убитыми, успевают выстрелить. В таком случае после первого залпа останется a-qb красных и b-pa синих, после второго: (1+pq)a-2qb красных и (1+pq)b-2pa синих, и т.д. (см таблицу).

\begin{tabular}{|c|c|c|} \hline №& красных & синих \\ \hline 0& a & b \\ \hline 1& a-qb & b-pa \\ \hline 2& (1+pq)a-2qb & (1+pq)b-2pa \\ \hline 3& $(1+3pq)a-(3q+pq^2)b$ & $(1+3pq)b-(3p+p^2q)a$ \\ \hline 4& $ (1+6pq+p^2q^2)a-(4q+4pq^2)b $ & $(1+6pq+p2q2)b-(4p+4p2q)a$ \\ \hline \end{tabular}

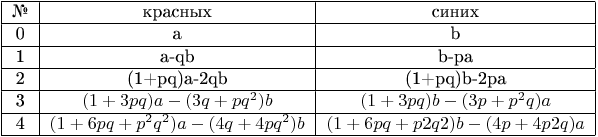
Выведем общую формулу из следующих рекуррентных соотношений:

$ \left\{ \begin{array}{l} a_{n+1}=a_n-qb_n,\\ b_{n+1}=b_n+pa_n,\\ a_0=a,\\ b_0=b; \end{array} \right. $



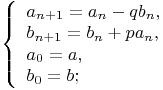
Тогда $a_{n+1}=a_n-qb_n=a_n+pqa_{n-1}-qb_{n-1}=a_n+pqa_{n-1}+pqa_{n-2}-qb_{n-2}...=a_n+pg\sum\limits_{i=0}^{n-1}{a_i}-qb$.
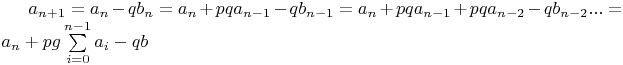Аналогично,
$b_{n+1}=...=b_n+pg\sum\limits_{i=0}^{n-1}{b_i}-pa$.

Попробуем теперь сначала уменьшить количество слагаемых в рекуррентных формулах, а затем выразить их из n.

$a_{n+2}=a_{n+1}+pqf_n+pg\sum\limits_{i=0}^{n-1}{a_i}-qb=a_{n+1}+(pq-1)a_n+a_n+pg\sum\limits_{i=0}^{n-1}{a_i}-qb=2a_{n+1}+(pq-1)a_n$

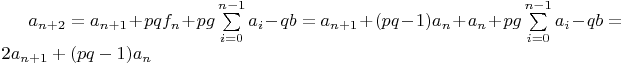
Теперь для разностного уравнения $a_{n+2}=2a_{n+1}+(pq-1)a_n$строим характеристическое уравнение: $x^2=2x+(pq-1)$и решаем его. Его корни $x_{1,2}=1\pm\sqrt{pq}$, значит, выражение имеет вид $a_n=k_1(1+\sqrt{pq})^n+k_2(1-\sqrt{pq})^n$. Подставив начальные условия для n=0 и n=1 имеем: $a_n=\frac{1}{2}\left(\left( a-b\sqrt{\frac{q}{p}}\right )\left( 1+\sqrt{pq} \right )^n+\left( a+b\sqrt{\frac{q}{p}} \right )\left( 1-\sqrt{pq}\right )^n \right)$
Аналогично:
$b_n=\frac{1}{2}\left(\left( b-a\sqrt{\frac{p}{q}}\right )\left( 1+\sqrt{pq} \right )^n+\left( b+a\sqrt{\frac{p}{q}} \right )\left( 1-\sqrt{pq}\right )^n \right)$
Таким образом получаются формулы, показывающие, как убывает количество солдат в сражении по принципам линейной тактики, если принять, что залпы даются сторонами одновременно. Единственный член формулы, ведущий к уменьшению величин a или b до отрицательных значений – это коэффициент $a-b\sqrt{\frac{q}{p}}$, соответственно, при $a\sqrt{p}>b\sqrt{q}$победят красные, а при $a\sqrt{p}<b\sqrt{q}$- синие (разумеется, учитывая вероятностный характер попаданий). Именно этот результат, кстати, можно получить и намного быстрее, выяснив, при каком условии отношение количества солдат не изменится после первого залпа: $\frac{a}{b}=\frac{a-qb}{b-pa}\Rightarrow\frac{a^2}{b^2}=\frac{q}{p}$

Для желающих поэкспериментировать прилагается также калькулятор в таблице Excel. Здесь вы задаёте начальные количества солдат, их точность и относительную скорострельность. Программа вычисляет, как будет изменяться количество солдат в ходе боя и кто в конечном итоге выйдет победителем.

Задайте вопрос на блоге о математике