- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона: 12↓
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
======= 143 ========
ММ143 (КГ11) (4 балла)
Девять из десяти ребер пятиугольной пирамиды имеют длину 1. В каком диапазоне может изменяться длина 10-го ребра?
====================
Решение
Очевидно, что возможны два случая: равны между собой все боковые ребра; равны между собой все ребра в основании.
Первый случай достаточно прозрачен. Вершины основания должны лежать на окружности. При этом десятое ребро может меняться от 0 (в случае когда пятиугольник в основании вырождается в квадрат) до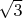 (когда вершины основания являются пятью вершинами правильного шестиугольника).
(когда вершины основания являются пятью вершинами правильного шестиугольника).
Поскольку в первом предельном случае пирамида становится четырехугольной, а во втором - плоской фигурой, крайние значения не достижимы и для длины десятого ребра получается интервал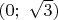 .
.
Значительно содержательнее второй случай. Легко видеть, что в этом случае пятиугольник в основании должен обладать осью симметрии. Кроме того, четыре из пяти вершин этого пятиугольника должны быть вершинами равнобочной трапеции. Переменную длину будет иметь ребро, соединяющее пятую вершину основания с вершиной трапеции.
Очевидно, что это ребро может быть сколь угодно коротким (нулевое значение достигается, когда вершины равнобочной трапеции в основании являются последовательными вершинами правильного шестиугольника, а угол при пятой вершине - развернутый).
Для нахождения наибольшего значения длины десятого ребра рассмотрим пятиугольник в основании пирамиды подробнее (см. рисунок).
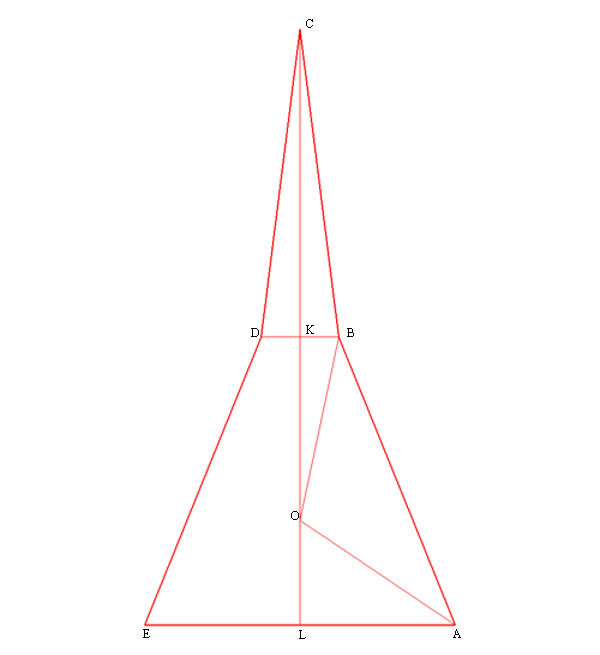
Пусть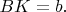 Тогда
Тогда 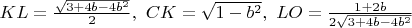 , а высота пирамиды
, а высота пирамиды 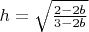 .
.
Дифференцируя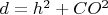 , как функцию от
, как функцию от 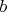 , находим значение
, находим значение 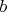 , при котором достигается максимальная длина десятого ребра
, при котором достигается максимальная длина десятого ребра 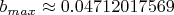 (точное значение, являющееся корнем уравнения 4-й степени можно выразить в радикалах, но выражение получается очень громоздким).
(точное значение, являющееся корнем уравнения 4-й степени можно выразить в радикалах, но выражение получается очень громоздким).
Легко убедиться, что это значение лежит в допустимых пределах изменения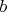 .
.
Учитывая, что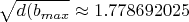 больше
больше 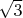 , окончательно получаем диапазон изменения длины десятого ребра пирамиды
, окончательно получаем диапазон изменения длины десятого ребра пирамиды ![$(0; \ \sqrt{d(b_{max})}]$ $(0; \ \sqrt{d(b_{max})}]$](http://dxdy.ru/math/dde1cfbbfd667a37aeb88376f9c7e04582.png) .
Обсуждение
.
Обсуждение
При уменьшении длины отрезка BD высота пирамиды монотонно увеличивается. Мне (и не только мне, но и ряду участников) сначала померещилось, что аналогично с уменьшением BD растет и CO. Это заблуждение нашло отражение в цене задачи.
Когда я, вскоре после публикации задачи, обнаружил свою ошибку, то сначала хотел внести исправление, увеличив цену задачи. Но затем решил не "светится" и увеличить балл за задачу лишь при при подведении итогов.
Награды
Отмеченная ошибка оказалась далеко не единственной. Некоторые участники не усмотрели возможности (а то и "усмотрели невозможность") изменения бокового ребра, другие рассматривали только выпуклые пятиугольники в основании, третьи наврали в вычислениях...
В результате баллы за задачу ММ143 распределились следующим образом:
Сергей Половинкин - 8 призовых баллов.
Андрей Халявин - 7 призовых баллов;
Дмитрий Пашуткин и Виктор Филимоненков - по 6 призовых баллов;
Кирилл Веденский - 5 призовых баллов;
Алексей Волошин Александр Ларин и iPhonograph - по 4 призовых балла;
Николай Дерюгин и Sirion - по 3 призовых балла;
Анатолий Казмерчук и Евгений Гужавин - по 2 призовых балла.
Эстетическая оценка - 4.6 балла
Разбор задачи ММ143 подготовил Владимир Лецко
ММ143 (КГ11) (4 балла)
Девять из десяти ребер пятиугольной пирамиды имеют длину 1. В каком диапазоне может изменяться длина 10-го ребра?
====================
Решение
Очевидно, что возможны два случая: равны между собой все боковые ребра; равны между собой все ребра в основании.
Первый случай достаточно прозрачен. Вершины основания должны лежать на окружности. При этом десятое ребро может меняться от 0 (в случае когда пятиугольник в основании вырождается в квадрат) до
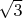 (когда вершины основания являются пятью вершинами правильного шестиугольника).
(когда вершины основания являются пятью вершинами правильного шестиугольника).Поскольку в первом предельном случае пирамида становится четырехугольной, а во втором - плоской фигурой, крайние значения не достижимы и для длины десятого ребра получается интервал
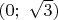 .
.Значительно содержательнее второй случай. Легко видеть, что в этом случае пятиугольник в основании должен обладать осью симметрии. Кроме того, четыре из пяти вершин этого пятиугольника должны быть вершинами равнобочной трапеции. Переменную длину будет иметь ребро, соединяющее пятую вершину основания с вершиной трапеции.
Очевидно, что это ребро может быть сколь угодно коротким (нулевое значение достигается, когда вершины равнобочной трапеции в основании являются последовательными вершинами правильного шестиугольника, а угол при пятой вершине - развернутый).
Для нахождения наибольшего значения длины десятого ребра рассмотрим пятиугольник в основании пирамиды подробнее (см. рисунок).

Пусть
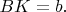 Тогда
Тогда 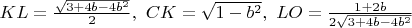 , а высота пирамиды
, а высота пирамиды 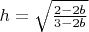 .
.Дифференцируя
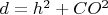 , как функцию от
, как функцию от 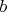 , находим значение
, находим значение 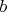 , при котором достигается максимальная длина десятого ребра
, при котором достигается максимальная длина десятого ребра 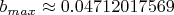 (точное значение, являющееся корнем уравнения 4-й степени можно выразить в радикалах, но выражение получается очень громоздким).
(точное значение, являющееся корнем уравнения 4-й степени можно выразить в радикалах, но выражение получается очень громоздким).Легко убедиться, что это значение лежит в допустимых пределах изменения
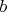 .
. Учитывая, что
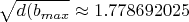 больше
больше 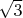 , окончательно получаем диапазон изменения длины десятого ребра пирамиды
, окончательно получаем диапазон изменения длины десятого ребра пирамиды ![$(0; \ \sqrt{d(b_{max})}]$ $(0; \ \sqrt{d(b_{max})}]$](http://dxdy.ru/math/dde1cfbbfd667a37aeb88376f9c7e04582.png) .
Обсуждение
.
ОбсуждениеПри уменьшении длины отрезка BD высота пирамиды монотонно увеличивается. Мне (и не только мне, но и ряду участников) сначала померещилось, что аналогично с уменьшением BD растет и CO. Это заблуждение нашло отражение в цене задачи.
Когда я, вскоре после публикации задачи, обнаружил свою ошибку, то сначала хотел внести исправление, увеличив цену задачи. Но затем решил не "светится" и увеличить балл за задачу лишь при при подведении итогов.
Награды
Отмеченная ошибка оказалась далеко не единственной. Некоторые участники не усмотрели возможности (а то и "усмотрели невозможность") изменения бокового ребра, другие рассматривали только выпуклые пятиугольники в основании, третьи наврали в вычислениях...
В результате баллы за задачу ММ143 распределились следующим образом:
Сергей Половинкин - 8 призовых баллов.
Андрей Халявин - 7 призовых баллов;
Дмитрий Пашуткин и Виктор Филимоненков - по 6 призовых баллов;
Кирилл Веденский - 5 призовых баллов;
Алексей Волошин Александр Ларин и iPhonograph - по 4 призовых балла;
Николай Дерюгин и Sirion - по 3 призовых балла;
Анатолий Казмерчук и Евгений Гужавин - по 2 призовых балла.
Эстетическая оценка - 4.6 балла
Разбор задачи ММ143 подготовил Владимир Лецко
Задайте вопрос на блоге о математике
