- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона (12)→
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона: 12↓
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
===============
MM123 (5 баллов)
Квадратная монета со стороной 1 см бросается случайным образом на лист бумаги, разлинованный квадратными клетками со стороной 2 см. Какая вероятность того, что монета попадёт целиком в клетку?
================
Решение
Бросание монеты можно описать математически как случайный выбор пары координат x и y, а также угла поворота монеты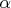
Понятно, что можно рассмотреть один квадрат со стороной 2 и координаты центра (точки пересечения диагоналей) монеты будут принимать значения от 0 до 2.
Выразим вероятность попадания монеты в ячейку от угла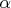 , который образует её сторона с горизонтальной линией разметки.
, который образует её сторона с горизонтальной линией разметки.
Всилу симметрии угол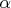 можно выбирать из диапазона от 0 до
можно выбирать из диапазона от 0 до 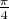 .
.
При угле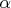 монету можно вписать в квадрат, со сторонами, параллельными сторонам ячейки и равными
монету можно вписать в квадрат, со сторонами, параллельными сторонам ячейки и равными 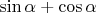 (такую картинку можно видеть в индийском доказательстве теоремы Пифагора). Центр этого квадрата совпадает с центром монеты. Пересечение описанного вокруг монеты квадрата с ячейкой равносильно пересечению самой монеты с ячейкой.
(такую картинку можно видеть в индийском доказательстве теоремы Пифагора). Центр этого квадрата совпадает с центром монеты. Пересечение описанного вокруг монеты квадрата с ячейкой равносильно пересечению самой монеты с ячейкой.

"Бесконфликтная" область для центра монеты будет иметь форму квадрата, расположенного в центре ячейки. Сторона этого квадрата составит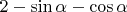 . Тогда вероятность того, что при данном угле
. Тогда вероятность того, что при данном угле 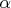 монета попадёт целиком в ячейку, равна отношению площадей "бесконфликтного" квадрата и всей ячейки
монета попадёт целиком в ячейку, равна отношению площадей "бесконфликтного" квадрата и всей ячейки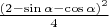
Взяв среднее интегральное этой дроби по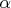 от 0 до
от 0 до 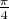 получим вероятность
получим вероятность 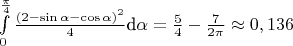 Обсуждение
Обсуждение
При упоминании случайного выбора сразу вспоминается классическая задача о произвольной хорде на окружности, решение которой зависит от того, как именно мы будем выбирать хорду. Здесь же процесс бросания определяется однозначно.
Ещё одна ассоциация с этой задачей - вычисление числа пи, бросая иголку на паркетный пол.
Для подтверждения уверенности в правильности решения можно воспользоваться моделированием процесса на компьютере. Кстати, я сам при её составлении и разработке черновика решения попался на то, что забыл поделить на длину отрезка, на котором берётся интеграл, и только результат моделирования заставил вспомнить об этом. Анализ решений показал, что в этом заблуждении я был не одинок.
Ещё одна причина, не позволившая одному из участников набрать максимальное количество баллов - выбор таких пределов интегрирования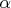 , при которых учитывается возможность пересечения с ячейкой только одной диагонали монеты.
, при которых учитывается возможность пересечения с ячейкой только одной диагонали монеты.
Некоторые участники брали кратные интегралы или разделяли "бесконфликтный" квадрат на области, вычисляя площади каждой из них отдельно, что увеличило число шагов в решении, но не помешало получить правильный ответ.
Собственно задача рождается, если, решив аналогичную задачу о бросании круглой монеты, задуматься: а что будет, если монета квадратная?
Награды
За правильное решение этой задачи Сергей Половинкин, Виктор Филимоненков, Эдвард Туркевич, Анатолий Казмерчук, Николай Дерюгин и Дмитрий Пашуткин получают по 5 призовых баллов. Алексей Волошин и Евгений Машеров получают по 3 призовых балла.
Эстетическая оценка задачи 4.3
================
Обзор задачи ММ123 подготовлен Алексеем Изваловым
MM123 (5 баллов)
Квадратная монета со стороной 1 см бросается случайным образом на лист бумаги, разлинованный квадратными клетками со стороной 2 см. Какая вероятность того, что монета попадёт целиком в клетку?
================
Решение
Бросание монеты можно описать математически как случайный выбор пары координат x и y, а также угла поворота монеты
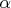
Понятно, что можно рассмотреть один квадрат со стороной 2 и координаты центра (точки пересечения диагоналей) монеты будут принимать значения от 0 до 2.
Выразим вероятность попадания монеты в ячейку от угла
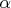 , который образует её сторона с горизонтальной линией разметки.
, который образует её сторона с горизонтальной линией разметки.Всилу симметрии угол
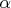 можно выбирать из диапазона от 0 до
можно выбирать из диапазона от 0 до 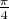 .
.При угле
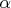 монету можно вписать в квадрат, со сторонами, параллельными сторонам ячейки и равными
монету можно вписать в квадрат, со сторонами, параллельными сторонам ячейки и равными 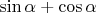 (такую картинку можно видеть в индийском доказательстве теоремы Пифагора). Центр этого квадрата совпадает с центром монеты. Пересечение описанного вокруг монеты квадрата с ячейкой равносильно пересечению самой монеты с ячейкой.
(такую картинку можно видеть в индийском доказательстве теоремы Пифагора). Центр этого квадрата совпадает с центром монеты. Пересечение описанного вокруг монеты квадрата с ячейкой равносильно пересечению самой монеты с ячейкой.
"Бесконфликтная" область для центра монеты будет иметь форму квадрата, расположенного в центре ячейки. Сторона этого квадрата составит
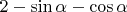 . Тогда вероятность того, что при данном угле
. Тогда вероятность того, что при данном угле 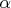 монета попадёт целиком в ячейку, равна отношению площадей "бесконфликтного" квадрата и всей ячейки
монета попадёт целиком в ячейку, равна отношению площадей "бесконфликтного" квадрата и всей ячейки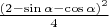
Взяв среднее интегральное этой дроби по
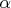 от 0 до
от 0 до 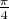 получим вероятность
получим вероятность 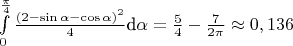 Обсуждение
Обсуждение При упоминании случайного выбора сразу вспоминается классическая задача о произвольной хорде на окружности, решение которой зависит от того, как именно мы будем выбирать хорду. Здесь же процесс бросания определяется однозначно.
Ещё одна ассоциация с этой задачей - вычисление числа пи, бросая иголку на паркетный пол.
Для подтверждения уверенности в правильности решения можно воспользоваться моделированием процесса на компьютере. Кстати, я сам при её составлении и разработке черновика решения попался на то, что забыл поделить на длину отрезка, на котором берётся интеграл, и только результат моделирования заставил вспомнить об этом. Анализ решений показал, что в этом заблуждении я был не одинок.
Ещё одна причина, не позволившая одному из участников набрать максимальное количество баллов - выбор таких пределов интегрирования
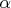 , при которых учитывается возможность пересечения с ячейкой только одной диагонали монеты.
, при которых учитывается возможность пересечения с ячейкой только одной диагонали монеты.Некоторые участники брали кратные интегралы или разделяли "бесконфликтный" квадрат на области, вычисляя площади каждой из них отдельно, что увеличило число шагов в решении, но не помешало получить правильный ответ.
Собственно задача рождается, если, решив аналогичную задачу о бросании круглой монеты, задуматься: а что будет, если монета квадратная?
Награды
За правильное решение этой задачи Сергей Половинкин, Виктор Филимоненков, Эдвард Туркевич, Анатолий Казмерчук, Николай Дерюгин и Дмитрий Пашуткин получают по 5 призовых баллов. Алексей Волошин и Евгений Машеров получают по 3 призовых балла.
Эстетическая оценка задачи 4.3
================
Обзор задачи ММ123 подготовлен Алексеем Изваловым
Задайте вопрос на блоге о математике
