- IV Интернет-олимпиада по математике/XIV тур Математического Марафона: 12↓
- XV тур математического марафона (12)→
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
======= 132 ========
ММ132 (5 баллов) (Здравствуй 2011-й)
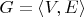 задан на множестве
задан на множестве 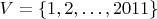 по правилу:
по правилу:  , где
, где  - фиксированное натуральное число, меньшее 1006.
- фиксированное натуральное число, меньшее 1006.
Сколько периферийных вершин может иметь граф G?
Примечание: Вершина графа называется периферийной, если ее эксцентриситет равен диаметру графа.
====================================
Решение
Рассмотрим три случая.
1.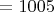 .
.
В этом случае граф не связен и, следовательно, не имеет периферийных вершин.
2.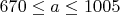 .
.
В этом случае диаметр графа равен 3.
Вершины эксцентриситета 3 будут сосредоточены на двух промежутках![$[2011-2a,\dots, a+1]$ $[2011-2a,\dots, a+1]$](http://dxdy.ru/math/af6a6708434bbdc494fd2ede9f2236a582.gif) и
и ![$[2011-a, \dots, 2a+1]$ $[2011-a, \dots, 2a+1]$](http://dxdy.ru/math/dfa85c5705186ff06eb5331e992de44882.gif) .
.
Например, кратчайший путь из вершины 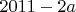 в вершину
в вершину 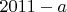 будет таким:
будет таким: 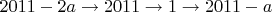 .
.
В то же время:
от вершин из промежутка![$[1, \dots, 2011-2a]$ $[1, \dots, 2011-2a]$](http://dxdy.ru/math/d3a47093ad83f37392f25a1a339009f782.gif) до любой вершины можно добраться либо за один шаг, либо через вершину
до любой вершины можно добраться либо за один шаг, либо через вершину 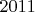 ;
;
аналогично не более чем за два шага можно добраться до любой вершины от вершин из промежутка![$[2a+2, \dots, 2011]$ $[2a+2, \dots, 2011]$](http://dxdy.ru/math/a0393ce240b7c05bc46506862523579d82.gif) .
.
Наконец, от вершин из промежутка![$[a+2, \dots, 2010-a]$ $[a+2, \dots, 2010-a]$](http://dxdy.ru/math/d0192a19342243d8a6841e1cd441406082.gif) можно добраться не более чем за два шага до любой вершины (через вершину
можно добраться не более чем за два шага до любой вершины (через вершину 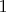 до вершин с бОльшими номерами и через вершину
до вершин с бОльшими номерами и через вершину 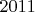 до вершин с меньшими номерами).
до вершин с меньшими номерами).
Таким образом, количество периферийный вершин равно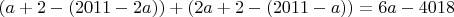 .
.
При значениях из рассматриваемого диапазона это дает нам следующий набор допустимых количеств периферийных вершин:
из рассматриваемого диапазона это дает нам следующий набор допустимых количеств периферийных вершин:  .
.
3.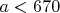
В этом случае каждая вершина имеет эксцентриситет 2. Поэтому все 2011 вершин будут периферийными.
Ответ::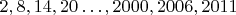 (или ни одной).
Обсуждение
(или ни одной).
Обсуждение
К моему удивлению, серьезные разногласия и путаницу вызвал случай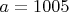 .
.
Полагаю, кроме варианта, приведенного в решении, имеет право на существование и такой: поскольку граф не связен, эксцентриситет каждой вершины бесконечен и все вершины являются периферийными.
Каким образом некоторые участники смогли насчитать 2008, 2010 или и вовсе одну периферийную вершину - для меня загадка.
Марафонцы существенно разошлись во мнениях, давая эстетическую оценку задаче ММ132. Для меня задачка любопытна немного неожиданным расположением периферийных вершин в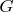 с точки зрения обычной упорядоченности вершин: и не по краям, и не в серединке.
с точки зрения обычной упорядоченности вершин: и не по краям, и не в серединке.
Награды
За решение задачи ММ132 Сергей Половинкин и Александр Ларин получают по 5 призовых баллов, Алексей Волошин и Анатолий Казмерчук - по 4 призовых балла, Дмитрий Пашуткин - 3 призовых балла, а Евгений Гужавин - 2 призовых балла.
Эстетическая оценка задачи 4.1 балла
====================================
Разбор задачи ММ132 подготовил Владимир Лецко
ММ132 (5 баллов) (Здравствуй 2011-й)
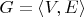 задан на множестве
задан на множестве 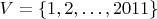 по правилу:
по правилу:  , где
, где  - фиксированное натуральное число, меньшее 1006.
- фиксированное натуральное число, меньшее 1006.Сколько периферийных вершин может иметь граф G?
Примечание: Вершина графа называется периферийной, если ее эксцентриситет равен диаметру графа.
====================================
Решение
Рассмотрим три случая.
1.
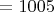 .
.В этом случае граф не связен и, следовательно, не имеет периферийных вершин.
2.
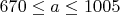 .
.В этом случае диаметр графа равен 3.
Вершины эксцентриситета 3 будут сосредоточены на двух промежутках
![$[2011-2a,\dots, a+1]$ $[2011-2a,\dots, a+1]$](http://dxdy.ru/math/af6a6708434bbdc494fd2ede9f2236a582.gif) и
и ![$[2011-a, \dots, 2a+1]$ $[2011-a, \dots, 2a+1]$](http://dxdy.ru/math/dfa85c5705186ff06eb5331e992de44882.gif) .
.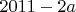 в вершину
в вершину 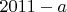 будет таким:
будет таким: 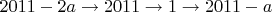 .
.В то же время:
от вершин из промежутка
![$[1, \dots, 2011-2a]$ $[1, \dots, 2011-2a]$](http://dxdy.ru/math/d3a47093ad83f37392f25a1a339009f782.gif) до любой вершины можно добраться либо за один шаг, либо через вершину
до любой вершины можно добраться либо за один шаг, либо через вершину 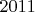 ;
;аналогично не более чем за два шага можно добраться до любой вершины от вершин из промежутка
![$[2a+2, \dots, 2011]$ $[2a+2, \dots, 2011]$](http://dxdy.ru/math/a0393ce240b7c05bc46506862523579d82.gif) .
.Наконец, от вершин из промежутка
![$[a+2, \dots, 2010-a]$ $[a+2, \dots, 2010-a]$](http://dxdy.ru/math/d0192a19342243d8a6841e1cd441406082.gif) можно добраться не более чем за два шага до любой вершины (через вершину
можно добраться не более чем за два шага до любой вершины (через вершину 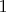 до вершин с бОльшими номерами и через вершину
до вершин с бОльшими номерами и через вершину 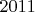 до вершин с меньшими номерами).
до вершин с меньшими номерами).Таким образом, количество периферийный вершин равно
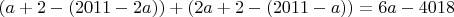 .
.При значениях
 из рассматриваемого диапазона это дает нам следующий набор допустимых количеств периферийных вершин:
из рассматриваемого диапазона это дает нам следующий набор допустимых количеств периферийных вершин:  .
.3.
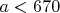
В этом случае каждая вершина имеет эксцентриситет 2. Поэтому все 2011 вершин будут периферийными.
Ответ::
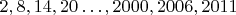 (или ни одной).
Обсуждение
(или ни одной).
ОбсуждениеК моему удивлению, серьезные разногласия и путаницу вызвал случай
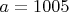 .
.Полагаю, кроме варианта, приведенного в решении, имеет право на существование и такой: поскольку граф не связен, эксцентриситет каждой вершины бесконечен и все вершины являются периферийными.
Каким образом некоторые участники смогли насчитать 2008, 2010 или и вовсе одну периферийную вершину - для меня загадка.
Марафонцы существенно разошлись во мнениях, давая эстетическую оценку задаче ММ132. Для меня задачка любопытна немного неожиданным расположением периферийных вершин в
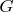 с точки зрения обычной упорядоченности вершин: и не по краям, и не в серединке.
с точки зрения обычной упорядоченности вершин: и не по краям, и не в серединке. Награды
За решение задачи ММ132 Сергей Половинкин и Александр Ларин получают по 5 призовых баллов, Алексей Волошин и Анатолий Казмерчук - по 4 призовых балла, Дмитрий Пашуткин - 3 призовых балла, а Евгений Гужавин - 2 призовых балла.
Эстетическая оценка задачи 4.1 балла
====================================
Разбор задачи ММ132 подготовил Владимир Лецко
Задайте вопрос на блоге о математике
