Задачи математических олимпиад: теория вероятности на Всеукраинской олимпиаде-2005

главная страница сайта Приглашение в мир математики

Задача.

Какова вероятность того, что при бросании монеты серия из трёх орлов подряд выпадет раньше, чем серия из двух решек подряд?

Эта задача была на Всеукраинской студенческой олимпиаде по математике в 2005 году в Севастополе. Оценивалась она в 12 баллов (всего за правильное решение всех 10 задач можно было получить, по-моему, 60 баллов).

Решение.

Будем обозначать выпадение орла как 0, а решку – как 1. Найдём сначала, сколько существует последовательностей из 0 и 1 длины n таких, которые заканчиваются ровно тремя нулями и не содержат других троек нулей и пар единиц. Обозначим это количество как Х(n), а выделенное жирным условие как Условие 1. Оно нам потом ещё пригодится.

Понятно, что для n=1 или 2 таких последовательностей не существует. Для n=3 возможна только единственная: 000. Далее цепочки длины n+1 можно получать из цепочек длины n, подставляя в качестве первого символа 0 или 1, с тем, чтобы продолжало выполняться Условие 1. Первые несколько шагов представлены в таблице.

Более наглядно процесс образования цепочек большей длины показывает вот такое дерево:

13

12

11

10

9

8

7

6

5

4

3

1–

–0\

–0–

–1–

–0\

–0–

–1–

–0\

–0–

–1–

–000

0–

–1/

0–

–1–

–0\

–0–

–1/

0\

–0–

–1/

1/

0–

–1–

–0\

–0–

–1–

–0\

–0–

–1/

0\

–0–

–1/

1/

0\

–0–

–1–

–0\

–0–

–1/

1/

1–

–0\

–0–

–1/

0–

–1/

n

X(n)

Возможные цепочки

1

0

-

2

0

-

3

1

000

4

1

1000

5

1

01000

6

2

101000; 001000

7

2

0101000; 1001000

8

3

00101000; 10101000; 01001000

9

4

100101000; 010101000; 001001000; 101001000

Поскольку всего цепочек из 0 и 1 длины n - $2^n$, то вероятность того, что три орла выпадут раньше двух решек после ровно n бросков, составляет $ \frac{X(n)}{2^n}$. Таким образом, для вычисления искомой вероятности требуется найти сумму $ \frac{X(1)}{2^1}+ \frac{X(2)}{ 2^2}+ \frac{X(3)}{ 2^3}+ \frac{X(4)}{ 2^4}+…$

Для этого сначала нужно найти общую формулу X(n). Введём 3 вспомогательных величины.
A(n) – количество цепочек из 0 и 1 длины n, которые удовлетворяют Условию 1 и начинаются с 00
B(n) – количество цепочек из 0 и 1 длины n, которые удовлетворяют Условию 1 и начинаются с 01
C(n) – количество цепочек из 0 и 1 длины n, которые удовлетворяют Условию 1 и начинаются с 10

При образовании цепочки длины n+1 перед каждой цепочкой, начинающейся с 00 для соблюдения Условия 1 можно ставить только 1, перед цепочками на 10 – только 0, а перед цепочками на 01 можно ставить и 0 и 1.

Получаем:
A(n+1) = B(n)
B(n+1) = C(n)
C(n+1) = A(n)+B(n)

Далее
A(n+2) = B(n+1) = C(n)
B(n+2) = C(n+1) = A(n)+B(n)
C(n+2) = A(n+1)+B(n+1) = B(n)+ C(n)

И ещё один шаг:
A(n+3) = B(n+2) = A(n)+B(n)
B(n+3) = C(n+2) = B(n)+ C(n)
C(n+3) = A(n+2)+B(n+2) = A(n)+B(n)+ C(n)

Тогда
X(n+3) = A(n+3)+B(n+3)+C(n+3) = 2A(n)+3B(n)+2C(n) = X(n+1)+X(n)
Мы получили для X(n) рекуррентную формулу.

К сожалению, я тогда не умел решать разностные уравнения, но интуитивно чувствовал, что, по аналогии с последовательностью Фибоначчи, X(n) можно в общем виде представить в виде суммы нескольких геометрических прогрессий, основанием одной из которых должен быть корень уравнения $\lambda^3=\lambda+1$, о чём и написал в решении. Тогда и сумма $\sum \limits_{n=1}^{\infty}{\frac{X(n)}{2^n}}$разложится в несколько геометрических прогрессий, которые затем легко свернутся.

За решение тогда поставили то ли 1 балл, то ли вообще 0. Я, разумеется, пошёл аппелировать. На аппеляции я в первый раз встретился с dm’ом, администратором научного форума http://dxdy.ru. Он разобрался в моём решении, сказал, что ход моих мыслей верный и рассказал, как нужно решать разностные уравнения. Другое дело, что дальнейшее решение по предполагаемому мной пути заняло бы время, намного большее уже потраченного. Однако свои 6 баллов я получил и в итоге вышел на 2е место с разрывом с первым в 1 балл (если бы не ступил при решении детской 4-х балльной задачи – было б первое).

Вечером пришла идея, как найти искомую сумму ряда, не решая характеристического уравнения $\lambda^3=\lambda+1$, а зная только произведение, сумму и сумму попарных произведений его корней из теоремы Виета. После достаточно объёмных преобразований сумма находилась. Я показал записи Дмитрию Юрьевичу и мы тогда решили, что это была бы интересная тема для статьи про нестандартное решение задачи на теорию вероятности.

Однако дома я всё откладывал оформление на потом и тема как-то забылась. Ну а сейчас наконец-то собрался и решил описать своё решение. Тем более что, позже покрутив эту задачу, я понял, как можно ещё проще найти сумму ряда.

Итак, дано:
X(n+3) = X(n+1)+X(n)
Найти:
$\sum \limits_{n=1}^{\infty}{\frac{X(n)}{2^n}}$

Пусть
$S= \frac{X(3)}{2^3}+ \frac{X(4)}{ 2^4}+ \frac{X(5)}{2^5}+\frac{X(6)}{2^6}+\frac{X(7)}{2^7}+…$
(члены X(1) и X(2), равные 0, просто опустим)

Разделим сумму на 4
$\frac{S}{4}=\frac{X(3)}{2^5}+ \frac{X(4)}{ 2^6}+ \frac{X(5)}{2^7}+\frac{X(6)}{2^8}+\frac{X(7)}{2^9}+…$

А теперь разделим её на 8
$\frac{S}{8}=\frac{X(3)}{2^6}+ \frac{X(4)}{ 2^7}+ \frac{X(5)}{2^8}+\frac{X(6)}{2^9}+\frac{X(7)}{2^10}+…$

И сложим последние 2 величины:
$\frac{S}{4}+\frac{S}{8}=\frac{X(3)}{ 2^5}+ \frac{X(3)+X(4)}{2^6}+ \frac{X(4) +X(5)}{ 2^7}+ \frac{X(5) +X(6)}{2^8}+\frac{X(6) +X(7)}{2^9}+\frac{X(7) +X(8)}{2^{10}}+…=\frac{X(3)}{ 2^5}+ \frac{X(6)}{2^6}+ \frac{X(7)}{ 2^7}+ \frac{X(8)}{2^8}+\frac{X(9)}{2^9}+\frac{X(10)}{2^{10}}+…=\frac{X(3)}{ 2^5}+S-\frac{X(3)}{2^3}- \frac{X(4)}{ 2^4}- \frac{X(5)}{2^5}$

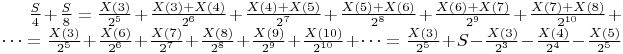
Подставив значения, решаем уравнение:
$\frac{S}{4}+\frac{S}{8}=\frac{1}{32}+S-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}$
Откуда S=0.3

Ответ
При бросании монеты с вероятностью 30% 3 орла подряд выпадут раньше двух решек подряд.

Вот так вот, через 3 с половиной года наконец-то выкладываю своё решение в виде статьи. Думаю теперь продолжать писать статьи на математические и околоматематические темы, идеи которых возникали давно, но всё откладывались в долгий ящик.

Задайте вопрос на блоге о математике