Задача о поиске радиоактивных шаров

Задача
Имеется 15 шаров. Среди них 2 радиоактивных. Имеется счётчик Гейгера. Его можно поднести к группе шаров и узнать, есть ли в ней радиоактивные (но неизвестно - сколько их). За сколько замеров можно найти оба радиоактивных шара в группе из 15 шаров?

Задачи подобного рода, в которых нужно, пользуясь прибором с конечным числом состояний, выделить искомые предметы из многих или упорядочить предметы, регулярно появляются на математических форумах. Они традиционно вызывают серьёзные затруднения при решении и споры в ходе его обсуждения.

Однако если знать общий подход, решение их достаточно легко.

Метод решения таких задач состоит из четырёх шагов, которые мы и рассмотрим.

Шаг 1: Определить количество вариантов ответа на задачу.
Перенумеруем шары числами от 1 до 15. Сколькими способами среди них могут располагаться два радиоактивных?
Первый радиоактивный шар может быть одним из пятнадцати. Второй – одним из четырнадцати. Всего 15*14=210 вариантов. Но т.к. каждая пара таким способом была подсчитана дважды (например, пары (1,2) и (2,1) – одна и та же пара шаров), то результат следует разделить на 2. Получим 210/2=105 вариантов.

Шаг 2: В какое наибольшее количество раз можно уменьшить количество возможностей, получив один результат измерения?
Т.к. счётчик может или запищать, или не запищать, то каждое измерение уменьшает количество возможностей не более чем вдвое.
В задачах о фальшивых монетах прибором выступают чаще всего весы, у которых может перевесить левая чаша, правая чаша или сохраниться равновесие – здесь неопределённость одним измерением снижается втрое.

Шаг 3. За какое количество измерений заведомо нельзя решить задачу?
Из 105 вариантов ответа, после первого измерения их останется не менее 53.
После второго – не менее 27.
После третьего – не менее 14.
После четвёртого – не менее 7.
После пятого – не менее 4.
После шестого – не менее 2.

Значит, за 6 измерений решить задачу невозможно. Попробуем это сделать за 7.

Шаг 4. Выберите предметы для измерения так, чтобы при любом его исходе ответ гарантированно находился за оставшиеся.

Поясним на примере.
Перед нами 15 шаров. Существует 105 возможных пар радиоактивных среди них.

Стоит ли для первого измерения выбирать один шар?
Если счётчик запищит, количество вариантов сократится до 14: это пары (1, 2), (1, 3), …, (1, 14). Один вариант из 14 можно найти за 4 измерения.
Н дозиметр не запищит в 105-14=91 случае, и если он не запищит, нам оставшихся шести замеров не хватит, чтобы найти радиоактивный.

Стоит ли для первого измерения брать два шара?
Счётчик запищит, если они оба радиоактивны (это 1 случай) или если радиоактивный только первый (это 13 случаев) или – только второй (ещё 13 случаев). Итого 27 случаев.

Не запищит же он в 105-27=78 случаях. Это всё равно больше, чем 64 – предельно возможное число вариантов, из которого можно выделить один за 6 измерений прибором, дающим один из двух вариантов ответа.

Рассуждая аналогично получим, что если сначала замерить три шара, 105 вариантов разделятся как 39+66, и мы опять не уложимся в оставшиеся 6 замеров.

Вот вариант с замером четырёх шаров выглядит перспективно:
Если прибор запищит, нужно будет за 6 измерений выбрать один вариант из 50, а если не запищит – из 55 (иначе говоря, во втором случае задача сведётся к поиску двух радиоактивных шаров из 11 за 6 измерений)

Но для задачи 2 из 11 за 6 нельзя подобрать такое измерение, которое бы 55 вариантов ответа разделило бы на две группы, каждая из которых содержит меньше 32 вариантов.

Итак, для первого замера надо брать 5 шаров.
Если не запищит, имеем задачу 2 из 10 за 6, которая решается легко.
Если же прибор запищит, то имеется 60 вариантов для пары радиоактивных шаров, которые можно представить в виде таблицы:

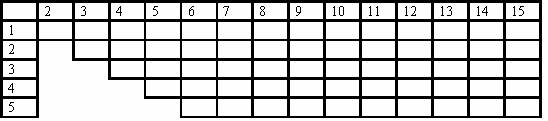
Повторяем Шаг 4
Каким измерением можно эти 60 вариантов разбить на 30+30 или 32+28?

Выбрав для второго замера шары 10, 11, 12, 13, 14, 15.

Тогда таблица разделится так:

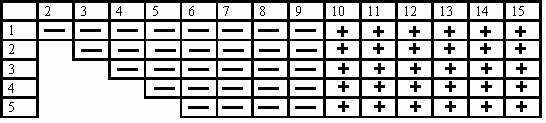
Плюсами обозначены варианты, на которые укажет положительный исход второго измерения, а минусами – отрицательный.

Рассмотрим каждый из них отдельно.

2+ - замеряем 13, 14, 15:

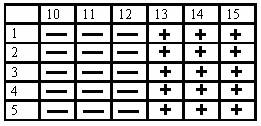
Т.к. структура вариантов одинакова, рассмотрим случай
2+3+
Замерим пару 1, 13.
На схеме показано, какие варианты расположения радиоактивных шаров дадут положительный, а какие – отрицательный результат.

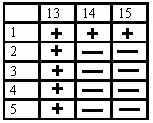
С 2+3+4– всё просто: мы имеем группы в 4 и в 2 шара, среди которых есть по одному радиоактивному. Из первой шар находится за 2, а из второй –за 1 измерение и мы укладываемся в 7 замеров.

При 2+3+4+ нужно измерить шар №1
При 5+ второй радиоактивный – среди 13, 14, 15 и находится ещё двумя измерениями.
При 5– радиоактивным будет шар №13, а второй находится среди 2, 3, 4, 5 и тоже находится двумя замерами.

Перейдём к ветке 2–
Казалось бы, стоит замерить 7, 8, 9 и разбить 30 вариантов на 15+15

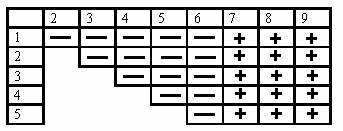
При 2-3+ действия были бы аналогичны 2+3+
Но при 2-3- мы не сможем эти 15 вариантов далее разбить на 7+8

Поэтому правильным шагом будет замер шаров 1 и 2

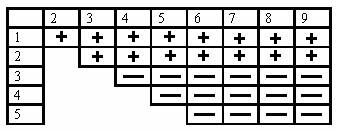
При 2-3+ замеряем шар №1 и далее находим второй радиоактивный из 8 или из 7 за 3 измерения.

При 2-3-замеряем шары 3 и 9

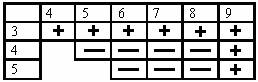
При 2-3-4+ измеряем 8 и 9.
При 5- шар № 3 наверняка радиоактивный, а второй нужно искать среди 4, 5, 6, 7 за 2 измерения.
При 5+ опять измеряем шар №3.
При 6+ второй радиоактивный или №8 или №9
При 6- радиоактивен №9, а второй - №4 или №5

При 2-3-4- измеряем шар №4.
При 5+ второй радиоактивный – среди шаров 5, 6, 7 или 8
При 5– шар №5 радиоактивен, а второй – среди 6, 7 или 8.

Итак, такой подход гарантирует, что среди 15 шаров пара радиоактивных будет найдена за 7 измерений.

И теперь задача для самостоятельного освоения метода.

Есть 5 шаров, среди которых 3 заряжены нейтрально, один – положительно и один – отрицательно. Есть прибор, который, будучи поднесённым к группе шаров покажет их общий заряд (он покажет 0 и если в группе не ни одного заряженного шара, и если они там оба).
За сколько измерений можно найти положительный и отрицательный шары в группе?