Два парома

Часто данная нестандартная задача на движение задаётся как «задача для третьего класса царской гимназии». Она также приводилась и у Гарднера. Однажды эта задача включалась в задания II городской олимпиады по математике для 11 класса. С решением не справился никто :(. А вот на сессии Малой академии наук её легко решили семиклассники.

Условие
Два парома отчаливают одновременно от противоположных берегов реки и встречаются на расстоянии 900 метров от левого берега. Прибыв к месту назначения, каждый паром сразу же отправляется обратно. Во второй раз паромы вновь встречаются в 300 метрах от правого берега. Чему равна ширина реки? Паромы двигались с постоянными скоростями.

1200 – это неправильный ответ :)

Решение
Изобразим схему движения паромов:

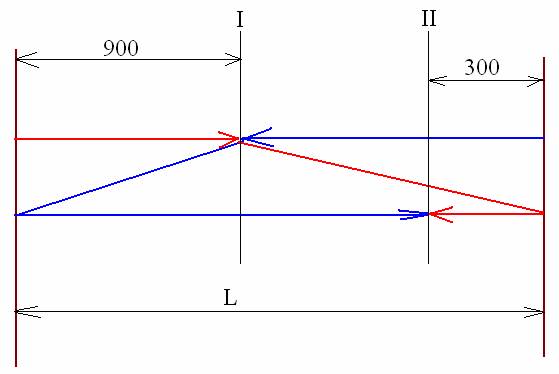
Алгебраическое решение
Пусть скорость первого парома равна u, а второго - v.
Отношение пройденных за одинаковые промежутки времени расстояний равно отношению скоростей. До первой встречи первый паром прошёл 900 метров, а второй – L-900 метров. Значит
.
С момента отчаливания до второй встречи первый паром прошёл L+300 метров, а второй – 2L-300 метров. И отношение этих расстояний также будет равно отношению скоростей.

Приравняем правые части:

Решаем пропорцию
900(2L-300)=(L+300)(L-900)
1800L-270000=-600L-270000
-2400L=0
Нулевой корень получившегося квадратного уравнения – посторонний, а вот
L=2400 –удовлетворяет условию.

Арифметическое решение
До первой встречи паромы вместе прошли расстояние, равное ширине реки.
От первой до второй встречи они прошли двойную ширину реки.
Т.к. паромы двигались равномерно, и до первой встречи красный паром прошёл 900 метров, то между первой и второй он прошёл 1800 метров. Однако из этих 1800 он 300 метров шёл в другую сторону. Так что ширина реки L=900+1800-300=2400 (м).

Ответ
2400 м