Задача о плитках домино

Задача

Сколькими способами можно покрыть полосу 2 х n клеток с помощью n плиток домино 1х2 так, чтобы полоса была покрыта полностью и никакая клетка не была покрыта дважды?

Решение

Пусть полоску 2xn можно покрыть соблюдая указанные условия R(n) способами. Рассмотрим, как может быть расположена плитка домино, покрывающая левый верхний угол полоски (Рис.1). Она может стоять вертикально или горизонтально (тогда и под ней должна находиться горизонтальная плитка). В первом случае оставшуюся часть полоски можно покрыть R(n-1) способами, а во втором - R(n-2) способами.

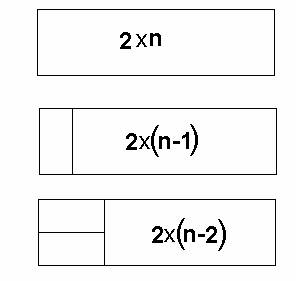
Рис 1. Покрытие полоски плитками домино.

Поскольку никакие способы покрытия полоски 2xn здесь не будут совпадать и все возможные способы перечислены, то получаем уравнение R(n)=R(n-1)+R(n-2). При этом R(1)=1, R(2)=2. Но в таком случае оказывается, что число способов покрытия полоски длины n плитками домино совпадает с n-м членом последовательности Фибоначчи, если её начинать не с пары единиц, а с 1 и 2..