Цепные дроби

Вместо обыкновенной дроби, с числителем и знаменателем, числа можно представлять в виде дробей цепных. Таких, у которых знаменатель сам содержит другую дробь, знаменатель которой - тоже дробь и так далее.

Превратить обыкновенную дробь в цепную легко - для этого нужно повторять действия взятия целой части числа и нахождения обратной величины от результата.

Пример: представить в виде цепной дроби число  



Таким образом, искомая цепная дробь имеет вид [1, 1, 4, 4]

То же самое можно сделать и с иррациональными числами, в виде обыкновенной дроби не выражающимися. Допустим, в цепную дробь мы хотим разложить число пи = 3,14159265358...

Для начала выделим целую часть:


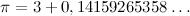
Затем дробную часть заменим дробью с единицей в числителе:


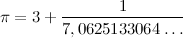
Теперь выполним это же действие с числом в знаменателе


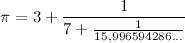
И ещё раз, и ещё:


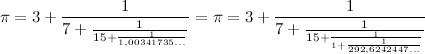
Полученная цепная дробь будет бесконечной и непериодической.

В более компактном виде это запишется как:

[3, 7, 15, 1, 292, 1, 1, 1, 2,...]

Кстати, при таком способе разложения скоро даёт о себе знать точность калькулятора, и начинаются ошибки. Например, если вычисления вести в Экселе, то для числа пи можно найти лишь 13 верных звеньев.

Оказывается, для квадратных корней существует способ получения цепной дроби любой длины, требующий лишь ручки и бумаги. Разложим с его помощью корень из 503.

 Для начала выделим в корне целую часть. Так как 22² = 484, а 23² = 529, то


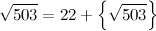
 Итак, искомое разложение начнётся как [22, ....]

 Превратим дробную часть в дробь с числителем 1:
 

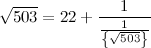
 Избавимся от иррациональности в знаменателе дроби, воспользовавшись тем, что:


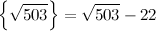
 Получим:


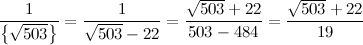
 Теперь выделим у дроби целую часть:
 

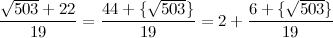
 Получили второй член разложения: [22, 2, ....] А в целом цепная дробь сейчас выглядит так:
 

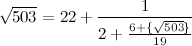
Перевернём теперь дробную часть ещё раз:


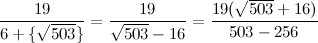
 Внимание! Здесь начинается особая математическая магия! Дело в том, что знаменатель обязательно должен разделиться на целый множитель числителя. Очень рекомендую это доказать - удовольствие гарантировано.

 Действительно, здесь тоже имеем:
 

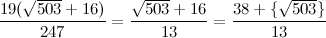
 И выделение целой части даёт нам новый член разложения: [22, 2, 2, ....]

 Вот новое звено цепной дроби:
   

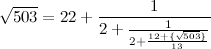
Данный процесс можно продолжать. Когда получим на каком-либо шаге дробь, которая получалась ранее (а мы обязательно получим такую, это тоже можно доказать), соответствующий участок разложения зациклится.

В итоге мы получим [22, (2, 2, 1, 21, 1, 2, 2, 44)].

 Вот так можно получить цепную дробь любого корня без каких-либо электронных вычислительных средств. А вообще, самый простой способ - это вбить в ВольфрамАльфе: continued fraction, а затем в новом открывшемся окошке написать sqrt(503)