Свойства числа 2013

Интересные свойства числа 2013, приводились нами по частям в блоге о занимательной математике "Десять букв", здесь же соберём их все вместе

• Во-первых, 2013 раскладывается на простые множители как: 2013 = 3 х 11 х 61 Таким образом, у числа 8 делителей: 1, 3, 11, 33, 61, 183, 671 и 2013
• Оно начинает серию из трёх идущих подряд чисел, имеющих 3 разных простых множителя (и, соответственно, 8 делителей): 2014 = 2 х 19 х 53 2015 = 5 х 13 х 31
• Понятно, что длиннее серий не существует, т.к. среди четырёх подряд идущих чисел одно будет делиться на 4 и, следовательно, иметь кратный простой множитель. Предыдущая такая серия начиналась с числа 1885, а следующая начнётся с 2665
• Число 2013 - это число Смита второй кратности. Для него сумма цифр всех простых множителей вдвое больше суммы цифр числа.
  2013 = 3 х 11 х 61 (2 + 0 + 1 + 3) х 2 = 3 + 1 + 1 + 6 + 1
• 2013 = 11 х 13² + 11 х 13 + 11
  
  Поэтому в тринадцатеричной системе число записывается как (BBB)₁₃
  В системе счисления по основанию 13 цифры А, В, С обозначают десятичные числа 10, 11 и 12.
• Запишем число 2013 в двоичной системе:
  (2013)₁₀=(11111011101)₂
  
  В троичной:
  (2013)₁₀=(2202120)₃
  
  И в пятеричной:
  (2013)₁₀=(31023)₅
  
  Так вот, во всех этих трёх представлениях суммы цифр одинаковы!
  
  1 + 1 + 1 + 1 + 1 + 0 + 1 + 1 + 1 + 0 + 1 =  2 + 2 + 0 + 2 + 1 + 2 + 0 = 3 + 1 + 0 + 2 + 3
  
• Сумма числа 2013 и его простых делителей 2013 + 3 + 11 + 61 = 2088
  равна сумме числа 2014 со своими простыми делителями: 2014 + 2 + 19 + 53 = 2088
• Интересная гипотеза существует относительно числа 2013. Если взять степень двойки и записать её в троичной системе, то там никогда не окажется 2013 нулей. 2012 нулей иможет быть, 2014 - тоже, а вот 213 нулей - никогда. (Однако точного доказательства ещё нет).

Красивые формулы, результатом которых является число 2013:
• 123 + 45 * 6 * 7 = 2013
• 1 + 2 * (3 + 4⁵) - 6 * 7 = 2013
• 333 + 3 + 333 + 3 + 333 + 3 + 333 + 3 + 333 + 3 + 333 = 2013
• 
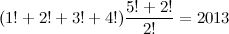
• Т.к. все цифры в записи числа 2013 меньше четырёх, его можно рассмотреть как запись некоторого числа в четверичной системе. Таким числом будет 2x4³+0x4²+1x4¹+3x4⁰=128+4+2=134.
• Ещё одно интересное свойство числа 2013 натолкнуло меня составить задачу по продолжению последовательности:
  9, 171, 27, 4, 9, 59, 18, 4, 18, 81, 9, 581,...