- Интересные свойства чисел: 6↓
- Математические сайты (7)→
- Логические игры (8)→
- О числе пи (5)→
- Форма расчёта налогов
- Превращаем цифры в забавных животных
- Как Ричард Фейнман победил японского вычислителя
- Как выводятся тригонометрические формулы
- Магические квадраты
- Цепные дроби
- Проблема 3x+1
- Вычислительные приёмы
- О сумме цифр, обобщённом признаке делимости и одной нерешённой задаче
- Генетический бассейн
- Совершенные, дружественные, и компанейские числа
- Механический генератор случайных чисел
- Что делать, если забыл математическую формулу? Вывести!
- Как писать самоописывающие тексты
- Нелинейная модель линейной тактики
- С Новым годом!!!
Традиционно в заданиях математических олимпиад некоторым образом фигурирует год её проведения. Так что в скором времени следует ожидать задач, затрагивающих число 2009. Мы заранее провели исследование и составили список некоторых интересных его свойств, надеемся, он окажется Вам полезным.
- Число 2009 раскладывается на простые множители следующим образом:

- Следовательно, число 2009 можно представить в виде разности квадратов целых чисел тремя способами:

- А в виде суммы квадратов число представляется единственным образом:

- Чтобы получить число 2009 в виде суммы кубов, потребуется минимум 4 слагаемых, и сделать это можно тремя способами:

- В виде суммы треугольных чисел (имеющих вид
 ) число 2009 можно представить 11-ю способами:
) число 2009 можно представить 11-ю способами:

- А в виде разности треугольных чисел число 2009 можно представить 6-ю способами:
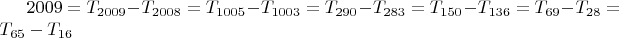
- 2009-е треугольное число равно 2 019 045
- Число 2009 входит в Пифагоровы тройки взаимно-простых чисел: (2009; 2018040; 2018041), (2009; 41160;41209), (360;2009;2041)
- Число 9002, образованное из 2009 обратной записью, также делится на 7:

- Число 2009 делится на сумму всех своих делителей, меньших корня из него: 1+7+41=49 и 2009 делится на 49
- 2009-е простое число равно 17471, это палиндром, оно одинаково читается как справа налево, так и слева направо
- Простыми также являются числа
 ,
,  ,
,  ,
,  ,
,  и
и 
- Рассмотрим процесс: берём натуральное число и прибавляем к нему сумму его цифр. Число 2009 в нём можно получить из самопорождённого (по Капрекару) числа 1693 за 19 шагов: 1693 - 1712 = 1693+(1+6+9+3) - 1723 = 1712+(1+7+1+2) - 1736 - 1753 - 1769 - 1792 - 1811 - 1822 - 1835 - 1852 - 1868 - 1891 - 1910 - 1921 - 1934 - 1951 - 1967 - 1990 - 2009.
- В другом процессе, рассмотренном индийским математиком Капрекаром, будем из числа, образованного цифрами четырёхзначного числа, записанными в порядке убывания, вычитать число, образованное теми же цифрами, но в порядке возрастания. К числу 6174, постоянной Капрекара, мы придём за 3 шага: К(2009) = 9200-0029=9171; К(9171) = 9711-1179=8532; К(8532) = 8532-2358=6174. К(6174) = 7641-1467=6174.
- В числе
 ровно 5765 цифр. Оно заканчивается пятьюстами нулями.
ровно 5765 цифр. Оно заканчивается пятьюстами нулями.
- Пожалуй, наиболее экзотический факт: оказывается, существует ровно 2009 5-мерных гексамино.
- Существует ровно 2009 Гамильтоновых графов с 8-ю вершинами. (В Гамильтоновых графах между каждыми двумя вершинами существует путь, проходящий через все остальные вершины ровно один раз)
Задайте вопрос на блоге о математике
