Задачи олимпиады Кенгуру, решения и ответы

Условия задач

Задача 21. Выпускник, 3й уровень, 2008 г.
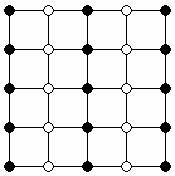
Случайным образом в решётке 3х4 точек выбрали три из них.

* * * *
* * * *
* * * *
Какова вероятность того, что эти точки будут лежать на одной прямой?
А:1/12; Б:1/11; В:1/16; Г:1/8; Д:1/4;

Задача 22. Юниор, 3й уровень, 2008 г.
Квадрат 4х4 разделили на 16 единичных квадратов. Найти максимально возможное количество диагоналей, которые можно провести в этих единичных квадратах так, чтобы они не имели общих точек (включая концы)
А:8; Б:9; В:10; Г:11; Д:12;

Задача 23. Кадет, 3й уровень, 2008 г.
Пусть m – произведение периметра треугольника на сумму трёх высот этого треугольника. Какое из высказываний ложно, если площадь этого треугольника равна 1?
А:m может быть больше 1000; Б:всегда m>6; В:m может равняться 18; Г:если треугольник правильный, то m>16; Д:m может быть меньше 12;

Задача 24. Школьник, 3й уровень, 2008 г.
Какое наибольшее количество цифр можно стереть в 1000-значном числе 20082008…2008, так, чтобы сумма оставшихся цифр равнялась 2008?
А:260; Б:510; В:746; Г:254; Д:130;

Задача 25. Малыш – 3,4, 3й уровень, 2008 г.
В коробке лежат 7 карточек с написанными на них числами от 1 до 7 (по одному числу на карточке). Первый мудрец наугад берёт три карточки из коробки, а второй – две (ещё две карточки остаются в коробке). Первый мудрец, глядя на свои карточки, говорит второму: «Я точно знаю, что сумма чисел  на твоих карточках чётная». Сумма чисел, записанных на карточках первого мудреца равняется:
А:6; Б:9; В:10; Г:12; Д:15;

Задача 26. Малыш – 2, 3й уровень, 2008 г.
Котик-Муркотик и Лисичка-Сестричка ловили рыбу. К ним подбежал голодный Волчик-Братик и спросил, много ли рыбы они поймали? Лисичка хитро ответила: у нас двоих рыб на 7 больше, чем у меня одной, а у одного из нас на 17 рыб меньше, чем у другого. Сколько рыбы словили вместе Котик-Муркотик и Лисичка-Сестричка?

А:10; Б:17; В:22; Г:27; Д:31;

Решения

Задача 21.
Подсчитаем, сколько троек точек могут образовать прямую линию. В каждом из трёх горизонтальных рядов таких троек будет по 4, также такими тройками будут 4 вертикальных и 4 диагональных ряда точек. Таким образом, всего троек точек, удовлетворяющих условию будет 20. Всего способов выбрать 3 точки из 12 будет 220. Таким образом, искомая вероятность равна 20/220=1/11.
Ответ: Б:1/11

Задача 22.
Раскрасим столбцы вершин единичных квадратов чёрным и белым цветами. Каждая диагональ единичного квадрата будет иметь концами точки разного цвета. Поэтому непересекающихся диагоналей может быть не более десяти. Один из вариантов представлен ниже.

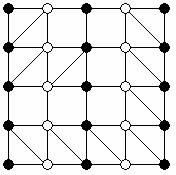
Ответ: В:10

Задача 23.
Поскольку , то ,  и . Тогда . Отсюда сразу видно, что если взять треугольник с площадью 1 и достаточно большим периметром, величина m может превысить 1000. Если раскрыть скобки, то получиться выражение вида m=6+f(a,b,c), принимающее значения, большие шести. Для правильного треугольника m=3*2*3=18>16. Следовательно, методом исключения, неверно пятое утверждение.
Ответ: Д:m может быть меньше 12;

Задача 24.
В данном числе последовательность 2008 повторяется 1000/4=250 раз. Сумма цифр этого числа равна 2500. Если вытереть 500 нулей, она не изменится. Таким образом, варианты А, Г и Д отметаем сразу, а вариант Б отметается после следующего размышления: даже если дополнительно вычеркнуть 10 восьмёрок, сумма оставшихся цифр уменьшится лишь на 80. Поэтому остаётся только вариант В, в целях экономии времени на олимпиаде его можно не проверять. А вообще, действительно: зачёркиваем 500 нулей и 246 двоек и сумма оставшихся цифр будет равна 2008.
Ответ: В:746

Задача 25.
Первый мудрец  будет точно знать, что сумма цифр на карточках сторого мудреца чётна лишь в том случае, если ему будет известно, что все оставшиеся числа – одной чётности. Следовательно, ему могли выпасть только карточки с числами 2, 4 и 6, их сумма равна 12. Данная задача проходила в 2008 году сквозь все классы и была использована для мониторинга умения совершать логические умозаключения. Наряду со стабильным ростом из класса в класс, тем не менее был отмечен общий низкий уровень данного умения.
Ответ: Г:12

Задача 26.
Если у них двоих рыб на 7 больше, чем у Лисички, то эти 7 рыб принадлежат Коту. И выходит, что у Лисички рыб на 17 больше, т.е. 24. Итого 31 рыба.
Ответ: Д:31

<Назад|Далее>