Задачи олимпиады Кенгуру, решения и ответы

Условия задач

Задача 1. Студент, 3й уровень, 1998 год
Сколько существует наборов из двух или более последовательных натуральных чисел, сумма которых равна 100?
А:1; Б:2; В:3; Г:4; Д:5;

Задача 2. Юниор, 3й уровень, 2003 год
Мы выписали все натуральные числа от однозначных до семизначных, в записи которых используются только 0 и 1. Сколько единиц мы записали?
А:128; Б:288; В:448; Г:512; Д:896;

Задача 3. Кадет, 3й уровень, 2005 год
Чему равняется ?
А:; Б: ; В: ; Г: ; Д: ;

Задача 4. Школьник, 3й уровень, 1999 год
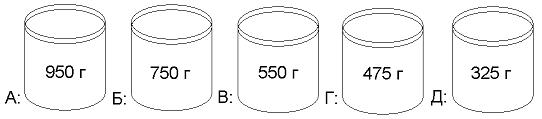
В каждом из пяти стаканов кофе, какао или молоко. Общий объём кофе вдвое больше объёма какао. Известно, что ни в каких трёх стаканах нет одинакового напитка. В каком стакане какао?

Задача 5. Малыш, 3й уровень, 2006 год
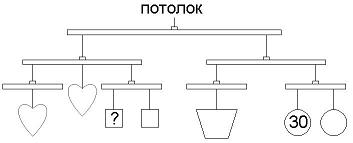
Детская игрушка подвешена к потолку и находится в равновесии. Одинаковые фигурки весят одинаково. Шарик весит 30 граммов. Сколько весит кубик, отмеченный знаком вопроса?

А:10г; Б:20г; В:30г; Г:40г; Д:50г;

Решения

Задача 1.
Сначала заметим, что суммой двух последовательных чисел число 100 не получить, т.к. из двух последовательных, одно будет чётным, а другой нечётным, и их сумма обязательно будет нечётным числом. Если же сложить 3 последовательных натуральных числа: n+n+1+n+2, то их сумма 3n+3 будет обязательно делиться на 3, следовательно, и здесь мы число 100 не получим. Для четырёх слагаемых окажется, что их сумма n+n+1+n+2+n+3=4n+6 даёт остаток 2 при делении на 4, а 100 делится на 4 нацело, итак, и здесь неудача.

Рассмотрим в общем случае сумму k последовательных натуральных чисел.
n+n+1+n+2+...+n+k-1=kn+k(k-1)/2
Отсюда видно, что при нечётных k сумма будет делиться на k, а при чётных k сумма k последовательных натуральных чисел будет давать остаток k/2 при делении на k, и, следовательно, будет делиться на k/2.

Выясним теперь, какое наибольшее количество последовательных слагаемых может образовать сумму в 100. Поскольку наименьшая по величине сумма из 14-ти слагаемых 1+2+...+14=14*15/2=105>100, то достаточно перебрать все k, не большие 13-ти. Из нечётных подходит только 5, т.к. на 7, 9, 11 или 13 число 100 не делится. Из чётных подходит только 8 (100=12*8+4).

Можно привести и соответствующие разбиения:
100=18+19+20+21+22
100=9+10+11+12+13+14+15+16
Итак, ответ Б:2 способа.
Кстати, интересно найти трёхзначное число, которое можно представить в виде суммы нескольких последовательных натуральных чисел наибольшим количеством способов. Но это уже совсем другая история :-).

Задача 2.
Хмм… интересно. Цифры 0 и 1, а также варианты ответа А:128 и Г:512 наталкивают на мысль об использовании двоичной системы счисления. И вправду, задачу можно переформулировать так: сколько единиц используется в двоичной записи всех чисел от 1 (даже от 0, на ответ это не повлияет) до 127? (от 0000000 до 1111111?)

Но ведь из этих 128-ми чисел в каждом из семи двоичных разрядов ровно у половины стоит единица, у другой половины – 0. Имеем 7*64=448 единиц во всех числах. Ответ В: 448.

Задача 3.
Первый вариант ответа  заставляет вспомнить о правильно-неправильных сокращениях и выносах из корня, когда выполняя неверные с математической точки зрения действия мы получаем верный результат. Однако вряд ли здесь это. Вариант больше похож на правду, учитывая, что для близких к данным в условии числам 300, 400 и 500 равенство выполняется (увеличенный в 100 раз египетский треугольник).

Стоп! А если мы египетский треугольник увеличим не в 100, а в 101 раз, что получим? Как раз эту тройку: 303, 404, 505. Значит, окончательно, ответ В:

Задача 4.
Вопрос звучит «В каком стакане какао?», значит, стакан с какао один. Тогда в двух из остальных четырёх стаканов кофе, и в двух – молоко.

В первом стакане какао быть не может, т.к. его объём максимальный и 2 других стакана не смогут занимать вдвое больший объём. А второй стакан (750г) подходит, тогда кофе будет в первом и третьем стаканах (950+550). Поскольку тест предполагает однозначный ответ, на этом можно и остановиться, сэкономив драгоценное время на решение других задач. Нам же с вами можно спокойно посидеть и убедиться, что действительно ни для какого из оставшихся стаканов нельзя найти двух других таких, чтобы они занимали вдвое больший объём. Ответ Б.

Задача 5.
Обратим внимание, что в формулировке задачи не говорится стандартная фраза «весом самой конструкции можно пренебречь». А ведь она и действительно не нужна – все перекладины уравновешивают друг друга и на решение не влияют.

Из правой части заметим, что трапеция равна по весу двум шарикам.
Из левой части одно сердечко равно по весу двум кубикам.
Значит, 6 кубиков равны четырём шарикам. 6 кубиков весят 120г, значит 1 кубик весит 20г. Ответ Б.

<Назад|Далее>