Задачи олимпиады Кенгуру, решения и ответы

Условия задач

Задача 95. Выпускник, 3й уровень, 2009 год
Ордината вершины параболы y=x²+bx+c равна -7 Сколько целых чисел может находиться между корнями уравнения x²+bx+с=0?

А:6 или 7; Б: 4 или 5; В: 5 или 6; Г: только 5; Д: только 6;

Задача 96. Юниор, 3й уровень, 2008 год
Кенгуру прыгает только вперёд на 1 или на 3 метра. Он хочет преодолеть ровно 10 метров. Сколькими способами он может это сделать?

А: 28; Б: 34; В: 35; Г: 55; Д: 56;

Задача 97. Кадет, 3й уровень, 2007 год
Дана числовая последовательность такая, что a₁=1, a₂=2, a₃=3, a_n+3= a_n+ a_n+1– a_n+2. Найдите a₂₀₀₇

А: -2006; Б: -2004; В: -2002; Г: 2008; Д: 2007;

Задача 98. Школьник, 3й уровень, 2007 год
Пять целых чисел написали по кругу так, что сумма никаких двух или трёх расположенных подряд не делится на 3. Сколько среди этих пяти чисел таких, которые делятся на 3?

А: 0; Б: 1; В: 2; Г: 3; Д: невозможно определить;

Задача 99. Малыш-3,4 классы, 3й уровень, 2008 год
Есть 5 коробок с карточками с буквами B, R, A, V, O.
В первой лежат B, V
Во второй лежат B, A, V, R
В третьей лежат A, B
В четвёртой лежит V
В пятой лежат B, R, A, V, O

Петя вытащил из коробок карточки так, чтобы в каждой коробке осталось по одной карточке и в разных коробках остались карточки с разными буквами. Какая буква останется во второй коробке?

А: B; Б: R; В: A; Г: V; Д: O;

Задача 100. Малыш-2 класс, 3й уровень, 2008 год
Маша подарила маме, бабушке, тёте и двум сёстрам по букету цветов. Цветы для сестёр и тёти были одного цвета. Известно, что бабушке она подарила не розы. Какой из этих букетов получила мама?

А: Жёлтые тюльпаны; Б: Розовые розы; В: Красные гвоздики; Г: Жёлтые розы; Д: Жёлтые гвоздики;

Решения:

Задача 95.
Рассмотрим параболу y=x²–7. Точки пересечения её с осью Ох имеют абсциссы , следовательно, расстояние между ними равно . При сдвиге параболы вдоль оси Ох, расстояние между корнями не поменяется, и т.к. , между корнями будут попадать 5 или 6 целых чисел.

Ответ В: 5 или 6;

Задача 96.
Есть 4 варианта представления числа 10 в виде суммы троек или единиц:
10=1+1+1+1+1+1+1+1+1+1=1+1+1+1+1+1+1+3=1+1+1+1+3+3=1+3+3+3
Первое разбиение предлагает всего один способ преодоления расстояния в 10 метров.
Во втором разбиении единственная тройка может быть одним из восьми слагаемых, что даёт 8 вариантов.
Из третьего разбиения можно получить  вариантов расположения прыжков в 3 метра.
В третьем разбиении единственная единица может быть одним из четырёх слагаемых, что даёт ещё 4 варианта.
Всего 1+8+15+4=28 вариантов.

Ответ А: 28;

Задача 97
Вычислим несколько членов последовательности: 1, 2, 3, 0, 5, -2, 7, -4, 9, -6, 11, -8, 13, -10, 15, -12, 17
Замечаем, что члены с нечётными номерами равны номеру. А члены с чётными номерами равны разности между числом 2 и номером.
a_2n+1=2n+1
a_2n=2-2n

Докажем то по индукции. Базу мы уже построили. Пусть это условие выполняется для всех чисел с номером, меньшим 2k. Тогда
a_2k= a_2k-3+ a_2k-2– a_2k-1 = 2k-3 + 2-(2k-2) – (2k-1) = 2-2k
a_2k+1= a_2k-2+ a_2k-1– a_2k = 2-(2k-2) + (2k-1) – (2-2k) = 2k+1
Доказано.

Следовательно, a₂₀₀₇ = 2007

Ответ Д: 2007;

Задача 98
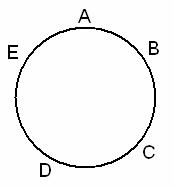Рассмотрим остатки от деления записанных чисел на 3.

Могут ли три из них быть равными 0? Нет, т.к. в таком случае 2 числа стояли бы рядом, и их сумма делилась бы на 3.

Что если два из остатков равняться 0? Да, но в таком случае между ними должен стоять некоторый нулевой остаток, скажем, 1. Пусть числа А и С делятся на 3, а В даёт остаток 1. Тогда 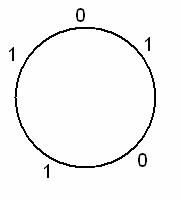остатки E и D должны равняться только единицам, иначе три рядом стоящих числа разделятся на 3. Получаем удовлетворяющее условию расположение.

 

Может ли только один из остатков равняться 0? Пусть А даёт остаток 0. Тогда у В и Е должны быть одинаковые ненулевые остатки, иначе или сумма одной из пар, или всех трёх чисел разделится на 3. Допустим, они равны 1.
Следовательно, ни один из остатков С и D не равен 2. Также они не могут одновременно равняться 1. Значит, один из них равен 0, а другой – 1. Но этот случай с двумя числами, делящимися на 2, мы уже рассмотрели.

Может ли ни одно число не делиться на 3? Нет, т.к. в таком случае найдётся три подряд стоящих одинаковых остатка, в сумме дающих делящееся на 3 число.

Следовательно, ровно 2 числа из пяти должны делиться на 3.

Ответ В: 2;

Задача 99.
Из четвёртой коробки ничего не нужно вытаскивать. Там останется V.
Значит, из первой нужно вытащить V и оставить В.
Тогда из третьей нужно вытащить В и оставить А.
И из второй нужно вытащить B, A, V и оставить R
Из пятой тогда Петя вытащит всё, кроме О.

Ответ Б: R;

Задача 100.
Три жёлтых букета: А, Г и Д получили тётя и сёстры. Т.к. бабушка получила не розы, то она получила гвоздики, а маме Маша подарила розовые розы.

Ответ Б: Розовые розы;

<Назад|Разбор типичных ошибок>