- IV Интернет-олимпиада по математике/XIV тур Математического Марафона: 12↓
- XV тур математического марафона (12)→
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
====================================
ММ131 (3 балла) (Прощай 2010-й)
Граф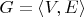 задан на множестве
задан на множестве 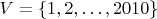 по правилу:
по правилу: 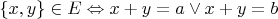 , где
, где  и
и 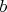 - фиксированные натуральные числа.
- фиксированные натуральные числа.
При каких и
и 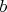 , граф
, граф 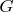 :
:
а) связен;
б) является деревом;
в) является цепью;
г) имеет циклы?
====================================
Решение
Ребро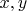 такое, что
такое, что 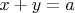 будем называть a-ребром, иначе b-ребром.
будем называть a-ребром, иначе b-ребром.
Ясно, что степень каждой вершины не больше 2, поскольку ей инцидентны не более одного ребра каждого типа.
При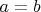 степени вершин G не больше 1. Такие графы не могу удовлетворять условиям пунктов а-г. Поэтому можно считать,
степени вершин G не больше 1. Такие графы не могу удовлетворять условиям пунктов а-г. Поэтому можно считать,  и
и 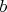 различны.
различны.
Допустим, что в графе есть циклы и вершина  - наибольшая (в смысле сравнения натуральных чисел) в одном из циклов. Cмежные ей вершины -
- наибольшая (в смысле сравнения натуральных чисел) в одном из циклов. Cмежные ей вершины -  и
и  . А этим вершинам, кроме
. А этим вершинам, кроме  , смежны вершины
, смежны вершины 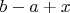 и
и 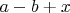 . Ясно. что одно из этих чисел больше
. Ясно. что одно из этих чисел больше  , что противоречит выбору
, что противоречит выбору  . Значит, G не имеет циклов ни при каких
. Значит, G не имеет циклов ни при каких  и
и 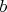 .
.
Для графа, степени вершин которого не превосходят 2, и не имеющего циклов, условия пунктов a-в равносильны. Для того, чтобы каждое из них выполнялось необходимо и достаточно, чтобы в G было 2009 ребер.
Легко видеть. что количество a-ребер в G равно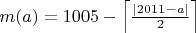 . Ясно,что
. Ясно,что 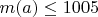 и максимум достигается лишь при
и максимум достигается лишь при 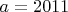 . Значение 1004 досгитается при
. Значение 1004 досгитается при 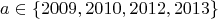
Аналогичные соотношения имеют место для b-ребер.
Поэтому общее число ребер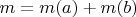 может достигать 2009 только тогда, когда одно
может достигать 2009 только тогда, когда одно  ,
, 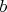 равно 2011. а другое отлчается от него не более чем на 2.
равно 2011. а другое отлчается от него не более чем на 2.
Ответ: Граф G связен, является деревом, является цепью тогда и только тогда. когда ровно одно из чисел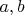 равно 2011, другое отличется от 2011 не более чем на 2. Граф G не содержит циклов ни при каких
равно 2011, другое отличется от 2011 не более чем на 2. Граф G не содержит циклов ни при каких  и
и 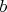 .
Обсуждение
.
Обсуждение
Как и в предыдущих марафонских задачах под графом я понимал классичиеский граф, в частности, не имеющий петель.
Нкоторые участники допускали наличие петель и получили несколько иные ответы. Их решения я считал верными. Самые предусмотрительные рассмотрели оба случая :)
Получаемые при подходящих a и b цепи можно выписать явно:
{a, b} = {2009, 2011}: 2009-2-2007-4-2005-6-...-3-2008-1-2010;
{a, b} = {2010, 2011}: 1005-1006-1004-1007-1003-...-2008-2-2009-1-2010;
{a, b} = {2011, 2012}: 1-2010-2-2009-3-2008-...-508-504-507-505-506;
{a, b} = {2011, 2013}: 1-2010-3-1008-5-...-6-2007-4-2009-2.
Разумеется, задача легко обобщается на граф с произвольным количеством вершин n.
При четных n (больших 2) для выполнения условий пунктов а-в одно из чисел a, b должно быть равно n+1, а другое отличаться от первого не более, чем на 2.
При нечетных n (больших 1) - a и b должны быть, двумя элементами множества {n, n+1, n+2}.
Награды
За правильное решение задачи Сергей Половинкин, Владислав Франк, Алексей Волошин. Евгений Гужавин, Анатолий Казмерчук и Дмитрий Пашуткин получают по 3 призовых балла, а Александр Ларин - 2 призовых балла.
Эстетическая оценка задачи 4.4 балла
====================================
Разбор задачи ММ131 подготовил Владимир Лецко
ММ131 (3 балла) (Прощай 2010-й)
Граф
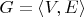 задан на множестве
задан на множестве 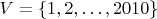 по правилу:
по правилу: 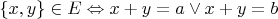 , где
, где  и
и 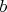 - фиксированные натуральные числа.
- фиксированные натуральные числа.При каких
 и
и 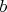 , граф
, граф 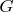 :
:а) связен;
б) является деревом;
в) является цепью;
г) имеет циклы?
====================================
Решение
Ребро
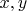 такое, что
такое, что 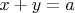 будем называть a-ребром, иначе b-ребром.
будем называть a-ребром, иначе b-ребром.Ясно, что степень каждой вершины не больше 2, поскольку ей инцидентны не более одного ребра каждого типа.
При
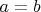 степени вершин G не больше 1. Такие графы не могу удовлетворять условиям пунктов а-г. Поэтому можно считать,
степени вершин G не больше 1. Такие графы не могу удовлетворять условиям пунктов а-г. Поэтому можно считать,  и
и 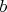 различны.
различны.  - наибольшая (в смысле сравнения натуральных чисел) в одном из циклов. Cмежные ей вершины -
- наибольшая (в смысле сравнения натуральных чисел) в одном из циклов. Cмежные ей вершины -  и
и  . А этим вершинам, кроме
. А этим вершинам, кроме  , смежны вершины
, смежны вершины 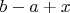 и
и 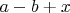 . Ясно. что одно из этих чисел больше
. Ясно. что одно из этих чисел больше  , что противоречит выбору
, что противоречит выбору  . Значит, G не имеет циклов ни при каких
. Значит, G не имеет циклов ни при каких  и
и 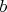 .
. Для графа, степени вершин которого не превосходят 2, и не имеющего циклов, условия пунктов a-в равносильны. Для того, чтобы каждое из них выполнялось необходимо и достаточно, чтобы в G было 2009 ребер.
Легко видеть. что количество a-ребер в G равно
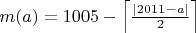 . Ясно,что
. Ясно,что 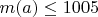 и максимум достигается лишь при
и максимум достигается лишь при 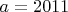 . Значение 1004 досгитается при
. Значение 1004 досгитается при 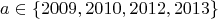
Аналогичные соотношения имеют место для b-ребер.
Поэтому общее число ребер
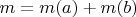 может достигать 2009 только тогда, когда одно
может достигать 2009 только тогда, когда одно  ,
, 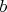 равно 2011. а другое отлчается от него не более чем на 2.
равно 2011. а другое отлчается от него не более чем на 2.Ответ: Граф G связен, является деревом, является цепью тогда и только тогда. когда ровно одно из чисел
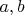 равно 2011, другое отличется от 2011 не более чем на 2. Граф G не содержит циклов ни при каких
равно 2011, другое отличется от 2011 не более чем на 2. Граф G не содержит циклов ни при каких  и
и 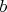 .
Обсуждение
.
ОбсуждениеКак и в предыдущих марафонских задачах под графом я понимал классичиеский граф, в частности, не имеющий петель.
Нкоторые участники допускали наличие петель и получили несколько иные ответы. Их решения я считал верными. Самые предусмотрительные рассмотрели оба случая :)
Получаемые при подходящих a и b цепи можно выписать явно:
{a, b} = {2009, 2011}: 2009-2-2007-4-2005-6-...-3-2008-1-2010;
{a, b} = {2010, 2011}: 1005-1006-1004-1007-1003-...-2008-2-2009-1-2010;
{a, b} = {2011, 2012}: 1-2010-2-2009-3-2008-...-508-504-507-505-506;
{a, b} = {2011, 2013}: 1-2010-3-1008-5-...-6-2007-4-2009-2.
Разумеется, задача легко обобщается на граф с произвольным количеством вершин n.
При четных n (больших 2) для выполнения условий пунктов а-в одно из чисел a, b должно быть равно n+1, а другое отличаться от первого не более, чем на 2.
При нечетных n (больших 1) - a и b должны быть, двумя элементами множества {n, n+1, n+2}.
Награды
За правильное решение задачи Сергей Половинкин, Владислав Франк, Алексей Волошин. Евгений Гужавин, Анатолий Казмерчук и Дмитрий Пашуткин получают по 3 призовых балла, а Александр Ларин - 2 призовых балла.
Эстетическая оценка задачи 4.4 балла
====================================
Разбор задачи ММ131 подготовил Владимир Лецко
Задайте вопрос на блоге о математике
