Решение задачи MM139 IV открытой интернет-олимпиады по математике: XIV тура Математического марафона

главная страница сайта Приглашение в мир математики
======= 139 ========

Задача ММ139 является развитием идеи задачи Кузнецова Сергея Тихоновича.
Оценка за решение этой задачи будет учитываться дважды: в основном Марафоне и в тематическом конкурсе.

ММ139 (МИ5) (7 баллов)

Кнопки калькулятора расположены так, как на цифровой клавиатуре:
\begin{tabular}{|c|c|c|} \hline 7 & 8 & 9 \\ \hline 4 & 5 & 6 \\ \hline 1 & 2 & 3 \\ \hline \multicolumn{2}{|c|}{0}\\ \cline{1-2} \end{tabular}
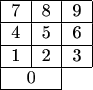
Назовём смежными те кнопки, которые имеют общую сторону или отрезок стороны (клавиша 0 смежна с клавишами 1 и 2).
Вначале на индикаторе число 0. Начинает игру Петя, прибавляя к нему любое (им выбранное) число от 0 до 9. Затем Вася прибавляет в полученному числу слагаемое, находящееся на смежной кнопке с той, которую нажимал Петя. Затем Петя делает свой ход, прибавляя число, смежное с нажатым Васей и т.д. Игра заканчивается, когда после очередного действия на индикаторе появится некоторое наперёд заданное число N (N>10). Если же некоторым ходом получено число, более N, игрок, сделавший такой ход, проигрывает.
Для каких N наибольшее число вариантов первого хода Пети приведёт его в дальнейшем к победе?

Решение
Для удобства построений переформулируем правила игры так: начинаем с некоторого N>10, и отнимаем от него числа от 0 до 9, пока не получится 0. Игрок, вынужденный получить отрицательное число, проигрывает.

Тогда из позиции (N,k) можно попасть во все позиции (N-d, d), где d - число на кнопке, смежной с k. Вот
список выигрышных и проигрышных позиций.

Таким образом, при N=43 или N=52 по 6 первых ходов Пети приведут его в дальнейшем к победе. Из остальных начальных позиций, больших десяти, таких ходов меньше. Обсуждение
Участники Марафона также заметили, что для всех N>2 существует универсальная выигрышная стратегия - нажимать на клавишу 0 до тех пор, пока не удастся закончить партию одним ходом или заставить противника следующим ходом сделать перебор.

Награды
За правильное решение задачи анатолий Казмерчук, Дмитрий Пашуткин, Алексей Волошин и Сергей Половинкин получают по 7 призовых баллов. Кирилл Веденский, решавший несколько другую задачу (когда только Пете нужно для победы получить N, а Васе - получить число, большее N), получает 6 баллов.

Эстетическая оценка задачи 4,5

Разбор задачи ММ139 подготовил Алексей Извалов

Задайте вопрос на блоге о математике