- Решения пробного тестирования по математике 2012: 7↓
- Разбор пробного тестирования по математике 2011 (11)→
- Как решать задачи пробного тестирования по математике - 2010 (11)→
- Ответы и решения ЗНО-2010 по математике (11)→
- Организационные вопросы тестирования (9)→
- Решения задач тестирования по математике 2009 (7)→
- Вторая часть ЗНО по математике
- Задание с сайта пробного ЗНО
- Решения задач пробного ЗНО 2014 по математике
- Стереометрия в пробном ЗНО 2014 по математике
- Решение задач про мост и про периодическую функцию
- Как решать задачи с корнями на ЗНО
- Все ответы и решения третьей части ЗНО
- Решение задачи ЗНО про график функции
- Задача на соответствие про преобразования плоскости
- Решение задачи по просьбе читателя
- Решения задач 17-20 ЗНО по математике
- ЗНО по математике: интеграл и метод интервалов
- Разбор задач первого дня тестирования (ЗНО) по математике
- Подготовка к Независимому внешнему оцениванию по математике 2010 года.
Задание 11. Системы уравнений
Сколько решений имеет система уравнений: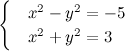 ?
?
Варианты ответа:
А ни одного; Б один; В два; Г три; Д более трёх;
Решение:
Сложив уравнения системы, получим: 2x2 = -2. Это уравнение решений в действительных числах не имеет, значит, и у исходной системы корней нет.
Ответ: А ни одного
Задание 12. Арифметическая прогрессия.
Из аэропорта авиарейсы по расписанию производятся каждые 10 минут. Первый самолёт вылетел в 6 часов утра. В котором часу по расписанию будет вылет 30-го самолёта?
Варианты ответа:
А 10 ч 40 мин; Б 10 ч 50 мин; В 11 ч 00 мин; Г 11 ч 30 мин; Д 12 ч 00 мин;
Решение:
Вылет 30-го самолёта произойдёт через 29 10-тиминутных интервалов, т.е. через 290 минут. Этот составит 4 часа 50 минут. Выходит, вылет запланирован на 10 ч 50 мин.
Ответ: Б 10 ч 50 мин Задание 13. Логарифм
Вычислите log216
Варианты ответа:
А ; Б
; Б  ; В 1; Г 8; Д 12;
; В 1; Г 8; Д 12;
Решение:
Преобразуем данный логарифм:
 (Потому, что показатель степени из основания логарифма выходит как знаменатель, а из логарифмируемого выражения – как числитель дроби-коэффициента перед логарифмом)
(Потому, что показатель степени из основания логарифма выходит как знаменатель, а из логарифмируемого выражения – как числитель дроби-коэффициента перед логарифмом)
Ответ: Б
Задание 14. Стереометрия. Пирамида. Объём
Сторона основания правильной четырёхугольной пирамиды равна 4 см, а объём – 64 см 3. Найдите высоту пирамиды.
текст
Варианты ответа:
А см; Б 4 см; В 8 см; Г 12 см; Д 16 см;
см; Б 4 см; В 8 см; Г 12 см; Д 16 см;
Решение:
Объём пирамиды втрое меньше произведения площади основания на высоту. Площадь основания равна 42 = 16 (см2). Значит, высота её равна (см)
(см)
Ответ: Г 12 см
Задание 15. Уравнения. Модули.
У какого из приведённых уравнений бесчисленное множество корней?
Варианты ответа:
А ; Б x = –x; В |x| = x; Г |–x| = 2; Д |x| = –3;
; Б x = –x; В |x| = x; Г |–x| = 2; Д |x| = –3;
Решение:
У первого уравнения корней нет совсем, т.к. косинус не может превосходить единицы. У второго единственный корень: x = 0. А вот третьему удовлетворяют все неотрицательные числа. Дальше перебирать не стоит – ответ найден.
Ответ: В |x| = x
Сколько решений имеет система уравнений:
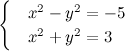 ?
?Варианты ответа:
А ни одного; Б один; В два; Г три; Д более трёх;
Решение:
Сложив уравнения системы, получим: 2x2 = -2. Это уравнение решений в действительных числах не имеет, значит, и у исходной системы корней нет.
Ответ: А ни одного
Задание 12. Арифметическая прогрессия.
Из аэропорта авиарейсы по расписанию производятся каждые 10 минут. Первый самолёт вылетел в 6 часов утра. В котором часу по расписанию будет вылет 30-го самолёта?
Варианты ответа:
А 10 ч 40 мин; Б 10 ч 50 мин; В 11 ч 00 мин; Г 11 ч 30 мин; Д 12 ч 00 мин;
Решение:
Вылет 30-го самолёта произойдёт через 29 10-тиминутных интервалов, т.е. через 290 минут. Этот составит 4 часа 50 минут. Выходит, вылет запланирован на 10 ч 50 мин.
Ответ: Б 10 ч 50 мин Задание 13. Логарифм
Вычислите log216
Варианты ответа:
А
Решение:
Преобразуем данный логарифм:
Ответ: Б
Задание 14. Стереометрия. Пирамида. Объём
Сторона основания правильной четырёхугольной пирамиды равна 4 см, а объём – 64 см 3. Найдите высоту пирамиды.
текст
Варианты ответа:
А
Решение:
Объём пирамиды втрое меньше произведения площади основания на высоту. Площадь основания равна 42 = 16 (см2). Значит, высота её равна
Ответ: Г 12 см
Задание 15. Уравнения. Модули.
У какого из приведённых уравнений бесчисленное множество корней?
Варианты ответа:
А
Решение:
У первого уравнения корней нет совсем, т.к. косинус не может превосходить единицы. У второго единственный корень: x = 0. А вот третьему удовлетворяют все неотрицательные числа. Дальше перебирать не стоит – ответ найден.
Ответ: В |x| = x
Задайте вопрос на блоге о математике
