Задачи олимпиады Кенгуру, решения и ответы

Условия задач

Задача 83. Выпускник, 3й уровень, 2009 год
Каково максимальное значение выражения
sin a cos b + sin b cos c + sin c cos d + sin d cos a
для действительных a, b, c, d?
А:1; Б:2; В:3; Г:4; Д: 8;

Задача 84. Юниор, 3й уровень, 2008 год
Известно, что х и у  - положительные действительные числа, и только одно из приведённых в ответах утверждений истинное. Какое?
А: x² > 2y²; Б: x > 2y; В: x > y; Г: x² > y²; Д: x > y²;

Задача 85. Кадет, 3й уровень, 2008 год
Некоторое количество прямых изобразили на бумаге так, что между ними есть углы величиной 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°. Найдите наименьшее количество прямых, для которых такое возможно.
А: 4; Б: 5; В: 6; Г: 7; Д: 8;

Задача 86. Школьник, 3й уровень, 2009 год
В стране Туфляндии у каждого жителя правая нога на один или на два размера больше левой. К сожалению, в магазине продаются пары обуви только одинакового размера. Чтобы сэкономить деньги, несколько друзей пошли в магазин и каждый из них купил одну пару обуви. Когда они обменялись обувью, один ботинок 36 размера и один ботинок 45 размера оказались лишними. Какое наименьшее количество человек могло быть в этой группе?
А: 5; Б: 6; В: 7; Г: 8; Д: 9;

Задача 87. Малыш-3,4 классы, 3й уровень, 2009 год
На клумбе расцвели цветы: белый, красный, синий и жёлтый. Пчела Майя подлетает к каждом цветку всего 1 раз. Сначала она летит к красному цветку, а затем – к остальным. Майя не может лететь с жёлтого цветка сразу на белый. Сколькими способами пчела Майя может посетить все 4 цветка?
А: 1; Б: 2; В: 3; Г: 4; Д: 6;

Задача 88. Малыш-2 класс, 3й уровень, 2008 год
Петя прибавляет 2, Назар отнимает 1, а Дима удваивает число. Каждый мальчик выполняет своё действие только один раз. В каком порядке им нужно выполнять эти действия, чтобы из 3 получить 9?

А: Дима, Петя, Назар;
Б: Петя, Дима, Назар;
В: Дима, Назар, Петя;
Г: Назар, Дима, Петя;
Д: Петя, Назар, Дима;

Решения:

Задача 83.
Выражение sin a cos b + sin b cos c + sin c cos d + sin d cos a можно рассмотреть как скалярное произведение 4-мерных векторов с координатами (sin a, sin b, sin c, sin d) и (cos b, cos c, cos d, cos a). По неравенству Коши-Буняковского, скалярное произведение векторов не превосходит произведения их модулей. Значит:

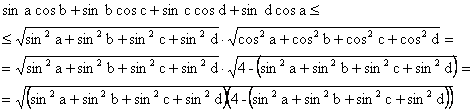
Применив теперь неравенство между средним геометрическим и средним арифметическим, получим:

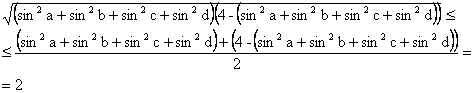
Взяв  получаем значение выражение, в точности равное двум.
Ответ Б:2;

Задача 84.
Установим, какие из приведённых соотношений взаимосвязаны.
А: x² > 2y²; => Г: x² > y²;
Б: x > 2y; => В: x > y;
В: x > y; <=> Г: x² > y²;
Выходит, утверждения А, Б, В, Г не могут быть единственными истинными, т.к. их истинность влечёт за собой истинность какого-нибудь ещё утверждения. Значит, они ложны, а единственно истинным будет утверждение x > y². Примером таких чисел будут
Д: x > y²;

Задача 85
Заметим, что среди прямых, две обязательно должны быть перпендикулярны. Если две перпендикулярные прямые пересечь ещё двумя, острых углов может получиться не более пяти, как в случае, когда ни одна из этих двух прямых не проходит через точку пересечения перпендикулярных (на рисунке), так и в других случаях.

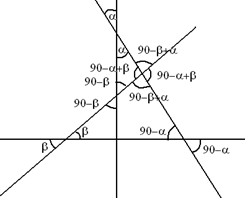
Имея же 5 прямых, мы можем построить требуемую конструкцию:

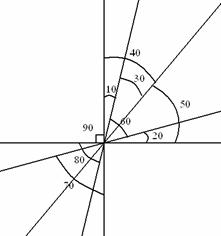
Ответ Б: 5;

Задача 86
Наименьшим количество покупателей будет, если у наибольшего их количества ноги различаются на 2 размера. Значит, это были люди с размерами: (45, 43), (43, 41), (41, 39), (39, 37) и (37, 36) – итого 5 человек. Но ответить 5 было бы опрометчиво. Ведь кроме обутых в итоге ботинок было куплено ещё 2 штуки. Значит, всего купили 6 пар ботинок и покупателей было шестеро.
Ответ Б: 6;

Задача 87.
Первый цветок она выбирает однозначно. Второй цветок может быть выбран одним из трёх способов:
Красный-Белый,
Красный -Синий или
Красный -Жёлтый.
Поскольку с жёлтого цветка нельзя лететь сразу на белый, получаем 5 способов для трёх цветков:
Красный - Белый - Жёлтый,
Красный - Белый - Синий,
Красный - Синий - Белый,
Красный - Синий - Жёлтый,
Красный - Жёлтый - Синий
Но среди этих способов один путь, а именно, Красный - Синий - Жёлтый – тупиковый, т.к. никакой цветок, кроме белого, не остаётся, а на него лететь нельзя. Остальные же 4 тройки дают нам 4 возможных маршрута облёта цветов:
Красный – Белый – Жёлтый – Синий,
Красный – Белый – Синий – Жёлтый,
Красный – Синий – Белый– Жёлтый,
Красный – Жёлтый – Синий– Белый
Ответ Г: 4;

Задача 88.
Поскольку 9=(3+2)*2-1, то сначала посчитать должен Петя, затем Дима, и потом - Назар;
Б: Петя, Дима, Назар;

<Назад|Далее>