- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона (12)→
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона: 12↓
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
===============
Задача ММ121 является прямым продолжением задачи ММ104.
Оценка за решение задачи ММ121 учитывается дважды в основном Марафоне и в тематическом конкурсе.
ММ121 (КГ-6) (8 баллов)
1. На сколько классов однотипных семиугольников разбиваются выпуклые семиугольники?
2. На сколько классов изотопных семиугольников разбиваются выпуклые семиугольники?
================
Решение

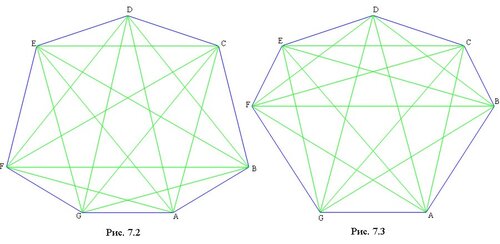
Опишем все классы изотопных выпуклых семиугольников. Начнем с рассмотрения семиугольника, изотопного правильному (рис. 7.1). Рассмотрим элементарные треугольники (на рисунке 7.1 они пронумерованы), примыкающие к единственному элементарному семиугольнику. Вариативность выпуклых семиугольников обеспечивается тем, что каждый из пронумерованных элементарных многоугольников может выродиться в точку или "инвертироваться". Например, перемещая вершины B и F можно получить из многоугольника, изображенного на рисунке 7.1, многоугольник, изображенный на рисунке 7.6, в котором исчез (выродился в особую точку) треугольник под номером 7. Продолжая перемещать вершины B и F можно получить семиугольник, изображенный на рисунке 7.2, в котором треугольник под номером 7 будет инвертирован, т.е. точка пересечения диагоналей AE и CG окажется по другую сторону от диагонали BF. При этом у соседних пронумерованных элементарных многоугольников изменится число сторон.
Базовым циклом выпуклого семиугольника назовем упорядоченный набор вида![$[a_1, a_2, \dots, a_7]$ $[a_1, a_2, \dots, a_7]$](http://dxdy.ru/math/dfb7c8497846f447b2584220c148e16182.gif) , где
, где 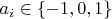 . Причем
. Причем 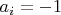 , если i-тый пронумерованный элементарный многоугольник инвертирован, и
, если i-тый пронумерованный элементарный многоугольник инвертирован, и 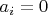 , если соответствующий элементарный многоугольник выродился в особую точку. Так, семиугольник, изображенный на рисунке 7.1, имеет базовый цикл [1,1,1,1,1,1,1], а семиугольник на рисунке 7.2 - [1,1,1,1,1,1, -1]. Будем считать два базовых цикла эквивалентными, если каждый из них получается из другого циклическим сдвигом и, возможно, изменением направления обхода. Очевидно, что справедливы следующие утверждения:
, если соответствующий элементарный многоугольник выродился в особую точку. Так, семиугольник, изображенный на рисунке 7.1, имеет базовый цикл [1,1,1,1,1,1,1], а семиугольник на рисунке 7.2 - [1,1,1,1,1,1, -1]. Будем считать два базовых цикла эквивалентными, если каждый из них получается из другого циклическим сдвигом и, возможно, изменением направления обхода. Очевидно, что справедливы следующие утверждения:
- каждый ноль в базовом цикле окружен единицами;
- каждая минус единица также окружена единицами;
- каждому классу эквивалентных базовых циклов, обладающих свойствами, отмеченными в предыдущих пунктах, соответствует ровно один класс изотопных выпуклых семиугольников;
- обратно, каждому классу изотопных выпуклых семиугольников соответствует свой класс эквивалентных базовых циклов, обладающих свойствами, указанными в первых двух пунктах.
Таким образом, подсчет количества классов изотопных выпуклых семиугольников сводится к подсчету числа классов эквивалентных базовых циклов. Последнее можно подсчитать, используя теорию перечисления Пойа. Однако в нашем случае проще получить ответ прямым перебором. В таблице 1 представлены с точностью до эквивалентности все базовые циклы, а на рисунках 7.1-7.15 - соответствующие семиугольники. Характеристический вектор семиугольника состоит всего из одной компоненты, значение которой равно разности числа 50 и числа элементарных многоугольников этого семиугольника. Поэтому мы не стали включать в таблицу информацию о характеристическом векторе.
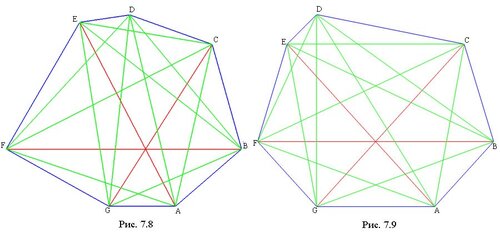
Поскольку изотопные многоугольники, очевидно, однотипны, для нахождения числа классов однотипных семиугольников достаточно рассмотреть по одному представителю из каждого класса изотопных. Такое рассмотрение показывает, что семиугольники на рисунках: 7.4 и 7.5, 7.7 и 7.8, 7.11 и 7.12, 7.13 и 7.14 - однотипны. Поэтому имеется всего 11 классов однотипных семиугольников.






Ответ: 1) 11 классов; 2) 15 классов. Обсуждение
Я попытался было замахнуться по подсчет или хотя бы не слишком грубую оценку числа классов изотопных (однотипных) восьмиугольников. Но задача оказалась крайне непростой. Типичная ситуация комбинаторного взрыва.
Награды
За правильное решение этой задачи Сергей Половинкин, Алексей Волошин и Анатолий Казмерчук получают по 8 призовых баллов. Николай Дерюгин, в решении которого имеются некоторые неточности, получает 6 призовых баллов.
Эстетическая оценка задачи - 4.4 балла
================
Обзор задачи ММ121 подготовлен Владимиром Лецко
Задача ММ121 является прямым продолжением задачи ММ104.
Оценка за решение задачи ММ121 учитывается дважды в основном Марафоне и в тематическом конкурсе.
ММ121 (КГ-6) (8 баллов)
1. На сколько классов однотипных семиугольников разбиваются выпуклые семиугольники?
2. На сколько классов изотопных семиугольников разбиваются выпуклые семиугольники?
================
Решение

Опишем все классы изотопных выпуклых семиугольников. Начнем с рассмотрения семиугольника, изотопного правильному (рис. 7.1). Рассмотрим элементарные треугольники (на рисунке 7.1 они пронумерованы), примыкающие к единственному элементарному семиугольнику. Вариативность выпуклых семиугольников обеспечивается тем, что каждый из пронумерованных элементарных многоугольников может выродиться в точку или "инвертироваться". Например, перемещая вершины B и F можно получить из многоугольника, изображенного на рисунке 7.1, многоугольник, изображенный на рисунке 7.6, в котором исчез (выродился в особую точку) треугольник под номером 7. Продолжая перемещать вершины B и F можно получить семиугольник, изображенный на рисунке 7.2, в котором треугольник под номером 7 будет инвертирован, т.е. точка пересечения диагоналей AE и CG окажется по другую сторону от диагонали BF. При этом у соседних пронумерованных элементарных многоугольников изменится число сторон.
Базовым циклом выпуклого семиугольника назовем упорядоченный набор вида
![$[a_1, a_2, \dots, a_7]$ $[a_1, a_2, \dots, a_7]$](http://dxdy.ru/math/dfb7c8497846f447b2584220c148e16182.gif) , где
, где 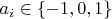 . Причем
. Причем 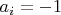 , если i-тый пронумерованный элементарный многоугольник инвертирован, и
, если i-тый пронумерованный элементарный многоугольник инвертирован, и 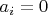 , если соответствующий элементарный многоугольник выродился в особую точку. Так, семиугольник, изображенный на рисунке 7.1, имеет базовый цикл [1,1,1,1,1,1,1], а семиугольник на рисунке 7.2 - [1,1,1,1,1,1, -1]. Будем считать два базовых цикла эквивалентными, если каждый из них получается из другого циклическим сдвигом и, возможно, изменением направления обхода. Очевидно, что справедливы следующие утверждения:
, если соответствующий элементарный многоугольник выродился в особую точку. Так, семиугольник, изображенный на рисунке 7.1, имеет базовый цикл [1,1,1,1,1,1,1], а семиугольник на рисунке 7.2 - [1,1,1,1,1,1, -1]. Будем считать два базовых цикла эквивалентными, если каждый из них получается из другого циклическим сдвигом и, возможно, изменением направления обхода. Очевидно, что справедливы следующие утверждения:- каждая минус единица также окружена единицами;
- каждому классу эквивалентных базовых циклов, обладающих свойствами, отмеченными в предыдущих пунктах, соответствует ровно один класс изотопных выпуклых семиугольников;
- обратно, каждому классу изотопных выпуклых семиугольников соответствует свой класс эквивалентных базовых циклов, обладающих свойствами, указанными в первых двух пунктах.
Таким образом, подсчет количества классов изотопных выпуклых семиугольников сводится к подсчету числа классов эквивалентных базовых циклов. Последнее можно подсчитать, используя теорию перечисления Пойа. Однако в нашем случае проще получить ответ прямым перебором. В таблице 1 представлены с точностью до эквивалентности все базовые циклы, а на рисунках 7.1-7.15 - соответствующие семиугольники. Характеристический вектор семиугольника состоит всего из одной компоненты, значение которой равно разности числа 50 и числа элементарных многоугольников этого семиугольника. Поэтому мы не стали включать в таблицу информацию о характеристическом векторе.
Поскольку изотопные многоугольники, очевидно, однотипны, для нахождения числа классов однотипных семиугольников достаточно рассмотреть по одному представителю из каждого класса изотопных. Такое рассмотрение показывает, что семиугольники на рисунках: 7.4 и 7.5, 7.7 и 7.8, 7.11 и 7.12, 7.13 и 7.14 - однотипны. Поэтому имеется всего 11 классов однотипных семиугольников.








Ответ: 1) 11 классов; 2) 15 классов. Обсуждение
Я попытался было замахнуться по подсчет или хотя бы не слишком грубую оценку числа классов изотопных (однотипных) восьмиугольников. Но задача оказалась крайне непростой. Типичная ситуация комбинаторного взрыва.
Награды
За правильное решение этой задачи Сергей Половинкин, Алексей Волошин и Анатолий Казмерчук получают по 8 призовых баллов. Николай Дерюгин, в решении которого имеются некоторые неточности, получает 6 призовых баллов.
Эстетическая оценка задачи - 4.4 балла
================
Обзор задачи ММ121 подготовлен Владимиром Лецко
Задайте вопрос на блоге о математике
