- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона (12)→
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона: 12↓
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
===============
ММ124 (4 балла)
Пусть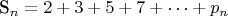 - сумма n первых простых чисел.
- сумма n первых простых чисел.
Доказать, что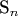 является простым тогда и только тогда, когда существует такое простое число q, что
является простым тогда и только тогда, когда существует такое простое число q, что 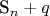 кратно
кратно 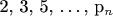 .
.
================
Решение
Приведу решение Виктора Филимоненкова.
1. Пусть такое число q для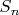 существует. Тогда
существует. Тогда 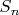 не делится ни на одно из чисел
не делится ни на одно из чисел 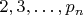 . Действительно, если
. Действительно, если 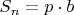 , где p - одно из первых n простых, и
, где p - одно из первых n простых, и 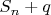 кратно p, то и q кратно p, а поскольку q простое, то q = p. Тогда
кратно p, то и q кратно p, а поскольку q простое, то q = p. Тогда  - делится на
- делится на  , в то время как
, в то время как 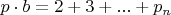 . То есть сумма n чисел, не меньших 2, лишь на одно слагаемое меньше их произведения, что для суммы первых простых чисел, очевидно, не верно начиная с
. То есть сумма n чисел, не меньших 2, лишь на одно слагаемое меньше их произведения, что для суммы первых простых чисел, очевидно, не верно начиная с 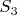 (для
(для 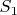 и
и 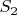 утверждение доказывается непосредственно).
утверждение доказывается непосредственно).
Но раз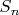 не делится на
не делится на 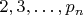 , то оно простое. Действительно,
, то оно простое. Действительно, 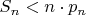 , а поскольку
, а поскольку 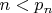 , то
, то 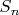 не делится на все простые, меньшие квадратного корня из
не делится на все простые, меньшие квадратного корня из 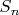 , то есть простое.
, то есть простое.
2. Пусть, наоборот,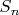 простое. Покажем, что простое q существует. Рассмотрим арифметическую прогрессию с первым членом
простое. Покажем, что простое q существует. Рассмотрим арифметическую прогрессию с первым членом 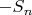 и разностью
и разностью  . Поскольку
. Поскольку 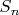 простое, то оно взаимно просто с
простое, то оно взаимно просто с  , и значит в этой прогрессии, по теореме Дирихле, есть бесконечное количество простых чисел. Любое из них годится в качестве q.
Обсуждение
, и значит в этой прогрессии, по теореме Дирихле, есть бесконечное количество простых чисел. Любое из них годится в качестве q.
Обсуждение
Для меня было неожиданностью, что ряд опытных, искушенных марафонцев испытывали некоторые затруднения при решении этой, на мой взгляд, простой задачи. (Конечно, теорема Дирихле о простых числах в арифметической прогрессии - утверждение нетривиальное. Но зато широко известное :)). При желании, я мог придраться к большему числу решений. Читая утверждения типа "составное число, меньшее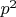 , не может иметь делителей, больших p", я был близок к "кровопролитию". Но сдержался :)
, не может иметь делителей, больших p", я был близок к "кровопролитию". Но сдержался :)
В OEIS последовательность простых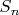 представлена под номером A013918.
представлена под номером A013918.
Интересно, конечно ли множество n, для которых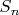 . Интуиция подсказывает, что:
. Интуиция подсказывает, что:
1) бесконечно;
2) доказательство первого пункта нетривиально :)
Награды
За правильное решение этой задачи Виктор Филимоненков, Эдвард Туркевич, Анатолий Казмерчук, Алексей Волошин и Mathusic получают по 4 призовых балла. Сергей Половинкин, Николай Дерюгин и Евгений Машеров получают по 2 призовых балла.
Эстетическая оценка задачи 4.3
================
Обзор задачи ММ124 подготовлен Владимиром Лецко
ММ124 (4 балла)
Пусть
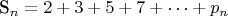 - сумма n первых простых чисел.
- сумма n первых простых чисел. Доказать, что
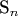 является простым тогда и только тогда, когда существует такое простое число q, что
является простым тогда и только тогда, когда существует такое простое число q, что 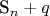 кратно
кратно 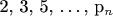 .
.================
Решение
Приведу решение Виктора Филимоненкова.
1. Пусть такое число q для
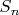 существует. Тогда
существует. Тогда 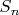 не делится ни на одно из чисел
не делится ни на одно из чисел 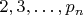 . Действительно, если
. Действительно, если 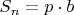 , где p - одно из первых n простых, и
, где p - одно из первых n простых, и 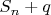 кратно p, то и q кратно p, а поскольку q простое, то q = p. Тогда
кратно p, то и q кратно p, а поскольку q простое, то q = p. Тогда  - делится на
- делится на  , в то время как
, в то время как 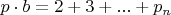 . То есть сумма n чисел, не меньших 2, лишь на одно слагаемое меньше их произведения, что для суммы первых простых чисел, очевидно, не верно начиная с
. То есть сумма n чисел, не меньших 2, лишь на одно слагаемое меньше их произведения, что для суммы первых простых чисел, очевидно, не верно начиная с 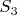 (для
(для 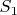 и
и 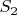 утверждение доказывается непосредственно).
утверждение доказывается непосредственно).Но раз
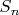 не делится на
не делится на 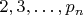 , то оно простое. Действительно,
, то оно простое. Действительно, 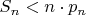 , а поскольку
, а поскольку 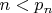 , то
, то 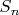 не делится на все простые, меньшие квадратного корня из
не делится на все простые, меньшие квадратного корня из 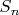 , то есть простое.
, то есть простое.2. Пусть, наоборот,
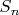 простое. Покажем, что простое q существует. Рассмотрим арифметическую прогрессию с первым членом
простое. Покажем, что простое q существует. Рассмотрим арифметическую прогрессию с первым членом 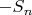 и разностью
и разностью  . Поскольку
. Поскольку 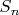 простое, то оно взаимно просто с
простое, то оно взаимно просто с  , и значит в этой прогрессии, по теореме Дирихле, есть бесконечное количество простых чисел. Любое из них годится в качестве q.
Обсуждение
, и значит в этой прогрессии, по теореме Дирихле, есть бесконечное количество простых чисел. Любое из них годится в качестве q.
Обсуждение Для меня было неожиданностью, что ряд опытных, искушенных марафонцев испытывали некоторые затруднения при решении этой, на мой взгляд, простой задачи. (Конечно, теорема Дирихле о простых числах в арифметической прогрессии - утверждение нетривиальное. Но зато широко известное :)). При желании, я мог придраться к большему числу решений. Читая утверждения типа "составное число, меньшее
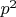 , не может иметь делителей, больших p", я был близок к "кровопролитию". Но сдержался :)
, не может иметь делителей, больших p", я был близок к "кровопролитию". Но сдержался :) В OEIS последовательность простых
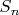 представлена под номером A013918.
представлена под номером A013918. Интересно, конечно ли множество n, для которых
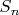 . Интуиция подсказывает, что:
. Интуиция подсказывает, что:1) бесконечно;
2) доказательство первого пункта нетривиально :)
Награды
За правильное решение этой задачи Виктор Филимоненков, Эдвард Туркевич, Анатолий Казмерчук, Алексей Волошин и Mathusic получают по 4 призовых балла. Сергей Половинкин, Николай Дерюгин и Евгений Машеров получают по 2 призовых балла.
Эстетическая оценка задачи 4.3
================
Обзор задачи ММ124 подготовлен Владимиром Лецко
Задайте вопрос на блоге о математике
