- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона (12)→
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона: 12↓
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
================
Оценка за решение задачи ММ128 учитывается дважды в основном Марафоне и в тематическом конкурсе.
ММ128 (КГ-10) (20 баллов)
На сколько классов изополярных восьмиугольников разбиваются выпуклые восьмиугольники?
================
Решение
Очевидно, что у выпуклого восьмиугольника может быть не более одного полюса второго порядка. А из рассуждений, приведенных при разборе задачи ММ102, следует, что общее число полюсов не может превышать девяти. Поэтому число классов изополярных восьмиугольников не превышает 19.
Ниже приведены представители 17 классов изополярных восьмиугольников. Для каждого случая приводится не только рисунок, но и координаты вершин, дабы желающие (если таковые найдутся :) ) могли убедиться, что все без обмана.
1.
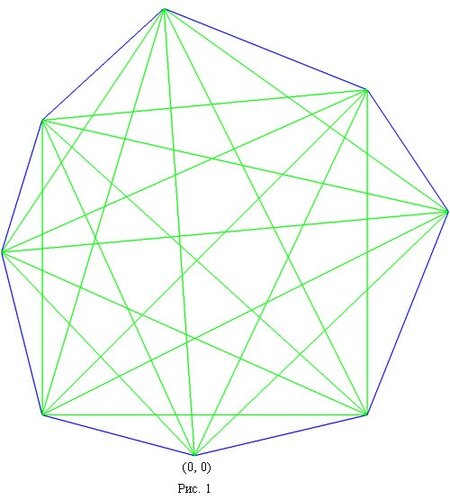
2.

3.

4.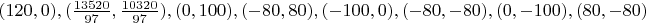
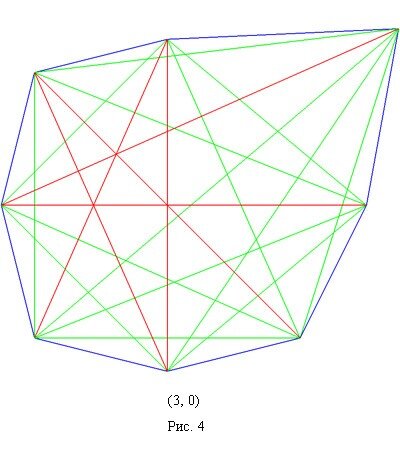
5.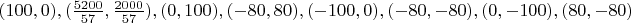
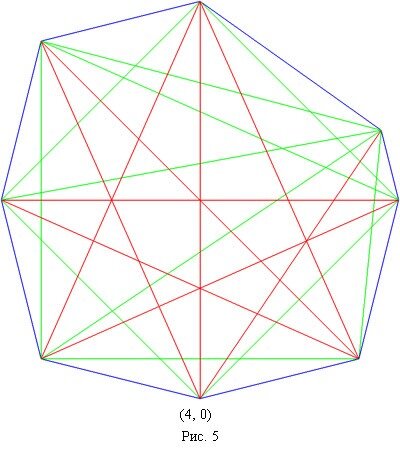
6.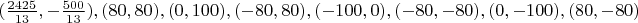

7.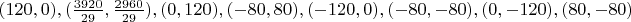

8.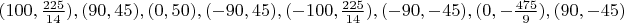
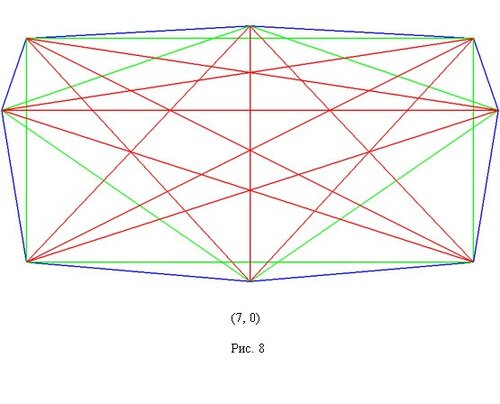
9.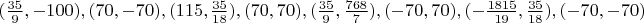

10.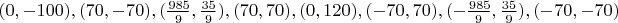

11.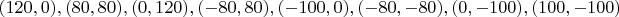

12.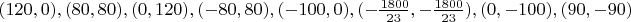
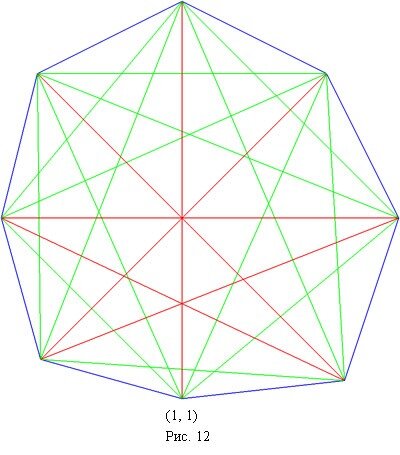
13.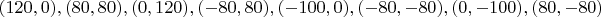

14.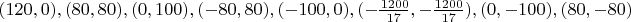

15.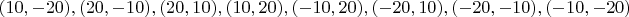
16.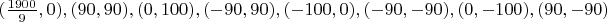

17.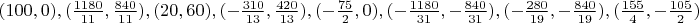

У меня нет строгого доказательства отсутствия классов с характеристическими векторами (5, 1) и (7, 1). Но есть соображения (не оставляющие лично у меня сомнения в том, что таких восьмиугольников не существует). Они приведены в обсуждении. Обсуждение
Вслед за Сергеем Половинкиным диагональ многоугольника буду называть i-диагональю, если между вершинами, которые она соединяет, (на ломаной из сторон, содержащей наименьшее число звеньев) расположено i вершин исходного многоугольника. Такая терминология представляется мне более удобной, чем та (с "короткими", "средними" и "длинными" диагоналями), которую я использовал раньше.
Ясно, что, если в восьмиугольнике есть полюс второго порядка, полюса первого порядка могут быть расположены либо на пересечении двух 2-диагоналей и одной 3-диагонали, либо на пересечении трех 2-диагоналей.
Координаты вершин многоугольника с рисунка 17 были получены следующим образом:
Несколько вершин (полагаю не сложно догадаться какие) и полюсов были подобраны заранее. Положение остальных зависело от неких параметров. Затем составлялась система, позволяющая найти такие значения параметров, при которых получался бы восьмиугольник, имеющий один полюс второго порядка и пять полюсов типа 2-2-3.
Однако, полученный таким образом восьмиугольник имеет не пять, а целых восемь полюсов первого порядка (все типа 2-2-3). Учитывая, что я специально строил восьмиугольник, не обладающий какими-либо очевидными симметриями, гипотеза о том, что еще целых три полюса образовались случайно, выглядит не слишком правдоподобной :) Тем более, что картина повторяется при построении восьмиугольника с другими начальным данными.
Полагаю, эти примеры убедительно свидетельствуют: наличие одного полюса второго порядка и пяти полюсов типа 2-2-3, автоматически влечет появление еще трех таких же полюсов.
Значит, надо искать среди многоугольников имеющих полюса типа 2-2-2.
В какой-то момент времени я был близок к мысли, что мне вот-вот удастся построить восьмиугольник с характеристическим вектором (5, 1). Казалось бы, достаточно немного "пошевелить" восьмиугольник, изображенный на рисунке 18-1, и цель будет накрыта!

И я "пошевелил". Результат Вы можете видеть на рисунке 18-2. Как только вершины были подвинуты так, чтобы близкие точки пересечения диагоналей стянулись в один полюс второго порядка, четыре полюса типа 2-2-3 и один полюс типа 2-2-2, как черт и табакерки выскочил еще один полюс типа 2-2-2, на который до "шевеления" не было даже намека.

Координаты вершин возникшего восьмиугольника с характеристическим вектором (6-1), на мой взгляд, исключают гипотезу случайного появления дополнительного полюса:
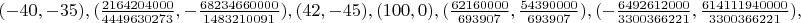
Восьмиугольник с рисунка 18-2 сыграл со мной злую шутку. Изучая его, я обнаружил, что все шесть полюсов первого порядка лежат на одном эллипсе (это достоверный факт, я подставлял координаты в уравнение). После этого я решил, что для строгого обоснования невозможности случаев (5, 1) и (7, 1) надо "копать" в сторону терем Паскаля, Брианшона, Штейнера еtc. И копал...
Но вот Анатолий Казмерчук прислал "обоснование" существования восьмиугольника типа (5, 1). Он поступил аналогично тому, как поступал я, с той разницей, что не стал отыскивать требуемое значение параметра, а лишь наметил план и указал, что по соображениям непрерывности такое значение обязательно найдется.
Наученный предыдущим опытом, я не сомневался, что одновременно с пятым полюсом первого порядка образуется и шестой, и что эти шесть полюсов лягут на один эллипс.
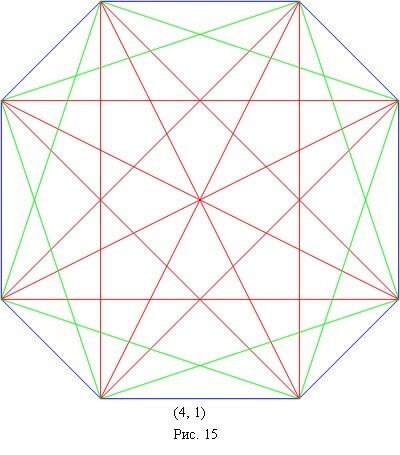
Первая гипотеза подтвердилась. А вот вторая... Здесь и подставлять ничего не надо, достаточно взглянуть на рисунок 19.

По традиции приведу координаты вершин: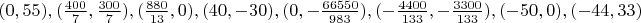
Мне по-прежнему не верится в случайность попадания шести полюсов многоугольника с рисунка 18-2 на один эллипс. Возможно так будет всегда, когда полюса типа 2-2-2 оказываются напротив друг друга. (Рисунок 16 показывает, что обращение этой гипотезы места не имеет.) Я наверняка постараюсь внести ясность в этот вопрос. Хотя построение примеров - вещь довольно утомительная. Даже с применением мат. пакетов.
Попытки построения восьмиугольника с характеристическим вектором (5, 1) и тремя полюсами типа 2-2-2 привели меня лишь к вырожденным "восьмиугольникам", у которых "склеиваются" несколько вершин.
Отмечу, что класс преобразований, не нарушающих изополярности восьмиугольника (даже имеющего много полюсов), довольно широк.
Например, ясно что проективное преобразование, сохраняя прямолинейность и инцидентность, переведет восьмиугольник в изополярный. (Если мы работаем на расширенной плоскости, то важно, чтобы прямая, образ которой будет несобственной прямой, не "цепляла" восьмиугольник.)
Однако даже в наиболее "узком" классе изополярных многоугольников с характеристическим вектором (8, 1) есть такие, которые не могут быть переведены друг в друга проективным преобразованием. Это следует хотя бы из того, что проективные преобразования сохраняют кривые второго порядка. В то же время, восьмиугольник с рисунка 17 не вписывается в кривую второго порядка, в отличие от правильного восьмиугольника, имеющего тот же характеристический вектор.
Алексей Волошин, единственный из участников представивший законченное описание представителей классов (с указанием координат всех вершин), отталкивался от различных правильных многоугольников. В результате, в его примерах координаты многих вершин иррациональны, в отличие от восьмиугольников, приведенных на рисунках 1-17.
Полагаю, что для произвольных выпуклых n-угольников ситуация такая же: в каждом классе изополярных многоугольников найдется представитель, у которого координаты всех вершин рациональны (если надо, то и целы).
В общем случае из изополярности восьмиугольников, разумеется, не следует их однотипность и, тем более. изотопность. Однако для восьмиугольников, насыщенных полюсами, картина иная. Так, все восьмиугольники с характеристическим вектором (8, 1), очевидно, изотопны. Восьмиугольники с характеристическим вектором (6, 1) уже могут быть не изотопны (см. рис. 18-2 и рис 19), но, по-видимому, всегда однотипны. Похоже , что однотипны, а возможно, и изотопны, будут и восьмиугольники с векторами (9, 0) и (8, 0).
Интересно, что в разбиении восьмиугольников с характеристическими векторами (8, 1), (6, 1) и (9, 0) встречаются только треугольники и четырехугольники.
Задачи нахождения чисел классов однотипных и изотопных восьмиугольников представляются весьма сложными. В любом случае счет идет на тысячи.
Награды
За решение задачи ММ128 Алексей Волошин получает 18 призовых баллов, Анатолий Казмерчук - 12 призовых баллов, а Сергей Половинкин - 10 призовых баллов.
Эстетическая оценка задачи 4.8 балла
================
Разбор задачи ММ128 подготовлен Владимиром Лецко.
Оценка за решение задачи ММ128 учитывается дважды в основном Марафоне и в тематическом конкурсе.
ММ128 (КГ-10) (20 баллов)
На сколько классов изополярных восьмиугольников разбиваются выпуклые восьмиугольники?
================
Решение
Очевидно, что у выпуклого восьмиугольника может быть не более одного полюса второго порядка. А из рассуждений, приведенных при разборе задачи ММ102, следует, что общее число полюсов не может превышать девяти. Поэтому число классов изополярных восьмиугольников не превышает 19.
Ниже приведены представители 17 классов изополярных восьмиугольников. Для каждого случая приводится не только рисунок, но и координаты вершин, дабы желающие (если таковые найдутся :) ) могли убедиться, что все без обмана.
1.
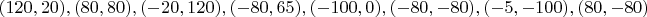

2.
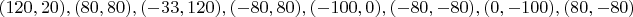

3.
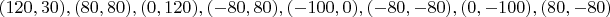

4.
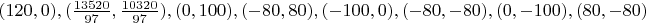

5.
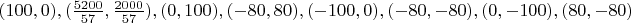

6.
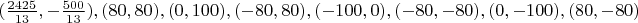

7.
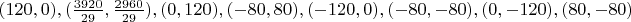

8.
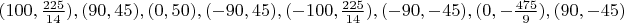

9.
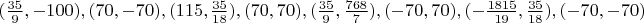

10.
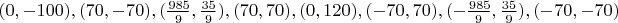

11.
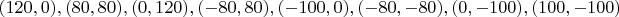

12.
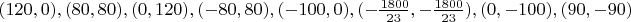

13.
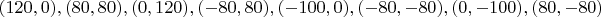

14.
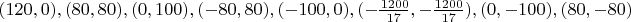

15.
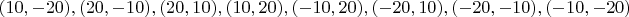

16.
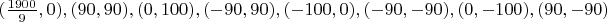

17.
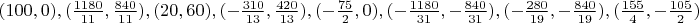

У меня нет строгого доказательства отсутствия классов с характеристическими векторами (5, 1) и (7, 1). Но есть соображения (не оставляющие лично у меня сомнения в том, что таких восьмиугольников не существует). Они приведены в обсуждении. Обсуждение
Вслед за Сергеем Половинкиным диагональ многоугольника буду называть i-диагональю, если между вершинами, которые она соединяет, (на ломаной из сторон, содержащей наименьшее число звеньев) расположено i вершин исходного многоугольника. Такая терминология представляется мне более удобной, чем та (с "короткими", "средними" и "длинными" диагоналями), которую я использовал раньше.
Ясно, что, если в восьмиугольнике есть полюс второго порядка, полюса первого порядка могут быть расположены либо на пересечении двух 2-диагоналей и одной 3-диагонали, либо на пересечении трех 2-диагоналей.
Координаты вершин многоугольника с рисунка 17 были получены следующим образом:
Несколько вершин (полагаю не сложно догадаться какие) и полюсов были подобраны заранее. Положение остальных зависело от неких параметров. Затем составлялась система, позволяющая найти такие значения параметров, при которых получался бы восьмиугольник, имеющий один полюс второго порядка и пять полюсов типа 2-2-3.
Однако, полученный таким образом восьмиугольник имеет не пять, а целых восемь полюсов первого порядка (все типа 2-2-3). Учитывая, что я специально строил восьмиугольник, не обладающий какими-либо очевидными симметриями, гипотеза о том, что еще целых три полюса образовались случайно, выглядит не слишком правдоподобной :) Тем более, что картина повторяется при построении восьмиугольника с другими начальным данными.
Полагаю, эти примеры убедительно свидетельствуют: наличие одного полюса второго порядка и пяти полюсов типа 2-2-3, автоматически влечет появление еще трех таких же полюсов.
Значит, надо искать среди многоугольников имеющих полюса типа 2-2-2.
В какой-то момент времени я был близок к мысли, что мне вот-вот удастся построить восьмиугольник с характеристическим вектором (5, 1). Казалось бы, достаточно немного "пошевелить" восьмиугольник, изображенный на рисунке 18-1, и цель будет накрыта!

И я "пошевелил". Результат Вы можете видеть на рисунке 18-2. Как только вершины были подвинуты так, чтобы близкие точки пересечения диагоналей стянулись в один полюс второго порядка, четыре полюса типа 2-2-3 и один полюс типа 2-2-2, как черт и табакерки выскочил еще один полюс типа 2-2-2, на который до "шевеления" не было даже намека.

Координаты вершин возникшего восьмиугольника с характеристическим вектором (6-1), на мой взгляд, исключают гипотезу случайного появления дополнительного полюса:
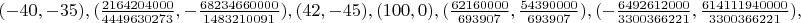
Восьмиугольник с рисунка 18-2 сыграл со мной злую шутку. Изучая его, я обнаружил, что все шесть полюсов первого порядка лежат на одном эллипсе (это достоверный факт, я подставлял координаты в уравнение). После этого я решил, что для строгого обоснования невозможности случаев (5, 1) и (7, 1) надо "копать" в сторону терем Паскаля, Брианшона, Штейнера еtc. И копал...
Но вот Анатолий Казмерчук прислал "обоснование" существования восьмиугольника типа (5, 1). Он поступил аналогично тому, как поступал я, с той разницей, что не стал отыскивать требуемое значение параметра, а лишь наметил план и указал, что по соображениям непрерывности такое значение обязательно найдется.
Наученный предыдущим опытом, я не сомневался, что одновременно с пятым полюсом первого порядка образуется и шестой, и что эти шесть полюсов лягут на один эллипс.
Первая гипотеза подтвердилась. А вот вторая... Здесь и подставлять ничего не надо, достаточно взглянуть на рисунок 19.

По традиции приведу координаты вершин:
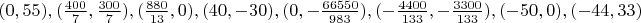
Мне по-прежнему не верится в случайность попадания шести полюсов многоугольника с рисунка 18-2 на один эллипс. Возможно так будет всегда, когда полюса типа 2-2-2 оказываются напротив друг друга. (Рисунок 16 показывает, что обращение этой гипотезы места не имеет.) Я наверняка постараюсь внести ясность в этот вопрос. Хотя построение примеров - вещь довольно утомительная. Даже с применением мат. пакетов.
Попытки построения восьмиугольника с характеристическим вектором (5, 1) и тремя полюсами типа 2-2-2 привели меня лишь к вырожденным "восьмиугольникам", у которых "склеиваются" несколько вершин.
Отмечу, что класс преобразований, не нарушающих изополярности восьмиугольника (даже имеющего много полюсов), довольно широк.
Например, ясно что проективное преобразование, сохраняя прямолинейность и инцидентность, переведет восьмиугольник в изополярный. (Если мы работаем на расширенной плоскости, то важно, чтобы прямая, образ которой будет несобственной прямой, не "цепляла" восьмиугольник.)
Однако даже в наиболее "узком" классе изополярных многоугольников с характеристическим вектором (8, 1) есть такие, которые не могут быть переведены друг в друга проективным преобразованием. Это следует хотя бы из того, что проективные преобразования сохраняют кривые второго порядка. В то же время, восьмиугольник с рисунка 17 не вписывается в кривую второго порядка, в отличие от правильного восьмиугольника, имеющего тот же характеристический вектор.
Алексей Волошин, единственный из участников представивший законченное описание представителей классов (с указанием координат всех вершин), отталкивался от различных правильных многоугольников. В результате, в его примерах координаты многих вершин иррациональны, в отличие от восьмиугольников, приведенных на рисунках 1-17.
Полагаю, что для произвольных выпуклых n-угольников ситуация такая же: в каждом классе изополярных многоугольников найдется представитель, у которого координаты всех вершин рациональны (если надо, то и целы).
В общем случае из изополярности восьмиугольников, разумеется, не следует их однотипность и, тем более. изотопность. Однако для восьмиугольников, насыщенных полюсами, картина иная. Так, все восьмиугольники с характеристическим вектором (8, 1), очевидно, изотопны. Восьмиугольники с характеристическим вектором (6, 1) уже могут быть не изотопны (см. рис. 18-2 и рис 19), но, по-видимому, всегда однотипны. Похоже , что однотипны, а возможно, и изотопны, будут и восьмиугольники с векторами (9, 0) и (8, 0).
Интересно, что в разбиении восьмиугольников с характеристическими векторами (8, 1), (6, 1) и (9, 0) встречаются только треугольники и четырехугольники.
Задачи нахождения чисел классов однотипных и изотопных восьмиугольников представляются весьма сложными. В любом случае счет идет на тысячи.
Награды
За решение задачи ММ128 Алексей Волошин получает 18 призовых баллов, Анатолий Казмерчук - 12 призовых баллов, а Сергей Половинкин - 10 призовых баллов.
Эстетическая оценка задачи 4.8 балла
================
Разбор задачи ММ128 подготовлен Владимиром Лецко.
Задайте вопрос на блоге о математике
