- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона: 12↓
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
======= 142 ========
ММ142 (4 балла)
Все 80 натуральных делителей натурального числа n расположили в порядке возрастания.
Оказалось, делители с первого по четвертый образуют геометрическую прогрессию,
делители с четвертого по седьмой - арифметическую прогрессию,
а восьмой делитель меньше 200. Найти n.
====================
Решение
Первые 4 делителя обязаны иметь вид: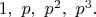
Учитывая, что 8-й делитель меньше 200, имеем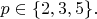
Пусть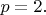 Тогда первый член арифметической прогрессии, которую образуют делители с 4-го 7-й, равен 8.
Тогда первый член арифметической прогрессии, которую образуют делители с 4-го 7-й, равен 8.
Разность прогрессии d не может быть четна, как в этом случае 6-й делитель равен 24. Но это невозможно, поскольку 3 не является делителем.
Если разность прогрессии нечетна, тогда 5-й делитель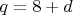 - наименьший нечетный простой делитель n.
- наименьший нечетный простой делитель n.
Поскольку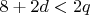 меньше, 6-й делитель равен 16. Но тогда 5-й равен 12, что невозможно.
меньше, 6-й делитель равен 16. Но тогда 5-й равен 12, что невозможно.
Итак, p не равно 2.
Пусть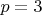 . Тогда все делители n нечетны и d обязано быть четным.
. Тогда все делители n нечетны и d обязано быть четным.
7-й делитель - кратен 3. Поэтому либо
- кратен 3. Поэтому либо 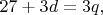 где
где 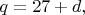 либо
либо 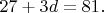
Легко проверить, что оба случая невозможны.
Остается случай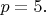 Тогда 4-й делитель равен 125, а делители с 5-го по 7-й (
Тогда 4-й делитель равен 125, а делители с 5-го по 7-й (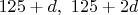 и
и 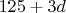 ) должны быть простыми.
) должны быть простыми.
Из последнего следует, что d обязано быть кратно 6. Если , то 8-й делитель больше 200.
, то 8-й делитель больше 200.
Итак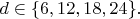
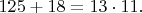 Поэтому d не может равняться 6 и 18.
Поэтому d не может равняться 6 и 18.
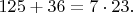 Поэтому d не может равняться 12.
Поэтому d не может равняться 12.
При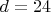 получаем три простых делителя 149, 173 и 197.
получаем три простых делителя 149, 173 и 197.
Для восьмого делителя, который меньше 200, остается одна возможность - 199.
Итак, мы уже имеем 5 различных простых сомножителей n. один из которых входит в разложение n не менее, чем в 3-й степени.
Это дает не менее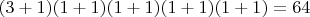 делителей.
делителей.
Если у n найдется еще один простой делитель или еще один из имеющихся делителей будет в ходить в разложение n в степени выше 1-й, общее число делителей превысит 80.
Остается единственная возможность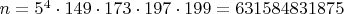 Обсуждение
Обсуждение
Задача не вызвала затруднений у участников. С ней успешно справились 15 человек (второй результат в истории Марафона).
Награды
За правильное решение задачи ММ142 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Николай Дерюгин, Дмитрий Пашуткин, Андрей Халявин, Евгений Машеров, Кирилл Веденский, Александр Ларин, Евгений Гужавин, Галина Крюкова. iPhonograph, Sirion и Umnik получают по 4 призовых балла.
Эстетическая оценка - 4.3 балла
Разбор задачи ММ142 подготовил Владимир Лецко
ММ142 (4 балла)
Все 80 натуральных делителей натурального числа n расположили в порядке возрастания.
Оказалось, делители с первого по четвертый образуют геометрическую прогрессию,
делители с четвертого по седьмой - арифметическую прогрессию,
а восьмой делитель меньше 200. Найти n.
====================
Решение
Первые 4 делителя обязаны иметь вид:
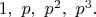
Учитывая, что 8-й делитель меньше 200, имеем
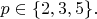
Пусть
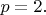 Тогда первый член арифметической прогрессии, которую образуют делители с 4-го 7-й, равен 8.
Тогда первый член арифметической прогрессии, которую образуют делители с 4-го 7-й, равен 8.Разность прогрессии d не может быть четна, как в этом случае 6-й делитель равен 24. Но это невозможно, поскольку 3 не является делителем.
Если разность прогрессии нечетна, тогда 5-й делитель
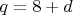 - наименьший нечетный простой делитель n.
- наименьший нечетный простой делитель n.Поскольку
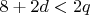 меньше, 6-й делитель равен 16. Но тогда 5-й равен 12, что невозможно.
меньше, 6-й делитель равен 16. Но тогда 5-й равен 12, что невозможно.Итак, p не равно 2.
Пусть
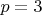 . Тогда все делители n нечетны и d обязано быть четным.
. Тогда все делители n нечетны и d обязано быть четным.7-й делитель
 - кратен 3. Поэтому либо
- кратен 3. Поэтому либо 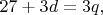 где
где 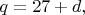 либо
либо 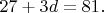
Легко проверить, что оба случая невозможны.
Остается случай
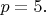 Тогда 4-й делитель равен 125, а делители с 5-го по 7-й (
Тогда 4-й делитель равен 125, а делители с 5-го по 7-й (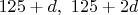 и
и 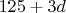 ) должны быть простыми.
) должны быть простыми.Из последнего следует, что d обязано быть кратно 6. Если
 , то 8-й делитель больше 200.
, то 8-й делитель больше 200.Итак
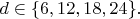
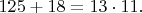 Поэтому d не может равняться 6 и 18.
Поэтому d не может равняться 6 и 18.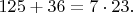 Поэтому d не может равняться 12.
Поэтому d не может равняться 12.При
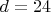 получаем три простых делителя 149, 173 и 197.
получаем три простых делителя 149, 173 и 197.Для восьмого делителя, который меньше 200, остается одна возможность - 199.
Итак, мы уже имеем 5 различных простых сомножителей n. один из которых входит в разложение n не менее, чем в 3-й степени.
Это дает не менее
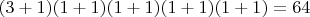 делителей.
делителей.Если у n найдется еще один простой делитель или еще один из имеющихся делителей будет в ходить в разложение n в степени выше 1-й, общее число делителей превысит 80.
Остается единственная возможность
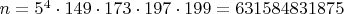 Обсуждение
ОбсуждениеЗадача не вызвала затруднений у участников. С ней успешно справились 15 человек (второй результат в истории Марафона).
Награды
За правильное решение задачи ММ142 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Николай Дерюгин, Дмитрий Пашуткин, Андрей Халявин, Евгений Машеров, Кирилл Веденский, Александр Ларин, Евгений Гужавин, Галина Крюкова. iPhonograph, Sirion и Umnik получают по 4 призовых балла.
Эстетическая оценка - 4.3 балла
Разбор задачи ММ142 подготовил Владимир Лецко
Задайте вопрос на блоге о математике
