- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона: 12↓
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
======= 146 ========
ММ146 (4 балла)
При каких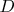 существуют графы диаметра
существуют графы диаметра 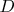 , у которых сумма квадратов степеней вершин равна
, у которых сумма квадратов степеней вершин равна 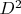 ?
?
====================
Решение
Сумма степеней вершин, а следовательно и сумма квадратов степеней вершин, любого графа - четна. Поэтому для нечетных D решений нет.
При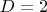 наименьшее значение суммы квадратов степеней вершин достигается у двухзвенной цепочки и равно 6. Поэтому
наименьшее значение суммы квадратов степеней вершин достигается у двухзвенной цепочки и равно 6. Поэтому 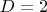 тоже не годится.
тоже не годится.
Не подходит и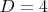 . У цепи длины 4 сумма квадратов степеней вершин - 14. Но добавление любой вершины (любых вершин) без изменения диаметра увеличивает минимум на
. У цепи длины 4 сумма квадратов степеней вершин - 14. Но добавление любой вершины (любых вершин) без изменения диаметра увеличивает минимум на  .
.
Покажем, что для всех четных  нужные графы имеются.
нужные графы имеются.
Возьмем цепь длины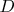 и будем добавлять к вершинам отличным от концевых висячие вершины: к одной -
и будем добавлять к вершинам отличным от концевых висячие вершины: к одной - 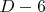 ; к одной - 2; к
; к одной - 2; к 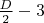 - по одной.
- по одной.
Сумма степеней вершин полученного графа составит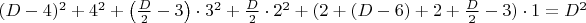 .
Обсуждение
.
Обсуждение
Существует много различных способов построения подходящих графов для четных . Вариант приведенный в решении предложен Кириллом Веденским и Анатолием Казмерчуком.
. Вариант приведенный в решении предложен Кириллом Веденским и Анатолием Казмерчуком.
Еще один универсальный метод предложен Виктором Филимоненковым: к одной из внутренних вершин вершин цепи длины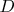 прицепим 2 висячие вершины, а к другой -
прицепим 2 висячие вершины, а к другой - 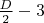 трехвзенных цикла.
трехвзенных цикла.
Другие подходы (в том числе и авторский) либо содержат исключения для малых значений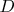 , либо варьируются, например, в зависимости от
, либо варьируются, например, в зависимости от 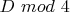 .
.
Уже не в первый раз (хотя я и не смог найти в архиве, когда был первый раз) некоторые марафонцы загадочным образом ухитряются найти диаметр графа, не являющегося связным. Насколько я в курсе (а я, полагаю, в курсе), диаметр (как и расстояние, через которое он вводится) определяется только для связного графа.
Награды
За правильное решение задачи ММ146 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Дмитрий Пашуткин, Кирилл Веденский и Андрей Халявин получают по 4 призовых балла. Александр Ларин получает 2 призовых балла.
Эстетическая оценка - 4.6 балла
Разбор задачи ММ146 подготовил Владимир Лецко
ММ146 (4 балла)
При каких
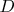 существуют графы диаметра
существуют графы диаметра 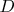 , у которых сумма квадратов степеней вершин равна
, у которых сумма квадратов степеней вершин равна 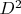 ?
?====================
Решение
Сумма степеней вершин, а следовательно и сумма квадратов степеней вершин, любого графа - четна. Поэтому для нечетных D решений нет.
При
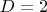 наименьшее значение суммы квадратов степеней вершин достигается у двухзвенной цепочки и равно 6. Поэтому
наименьшее значение суммы квадратов степеней вершин достигается у двухзвенной цепочки и равно 6. Поэтому 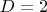 тоже не годится.
тоже не годится. Не подходит и
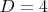 . У цепи длины 4 сумма квадратов степеней вершин - 14. Но добавление любой вершины (любых вершин) без изменения диаметра увеличивает минимум на
. У цепи длины 4 сумма квадратов степеней вершин - 14. Но добавление любой вершины (любых вершин) без изменения диаметра увеличивает минимум на  .
. нужные графы имеются.
нужные графы имеются.Возьмем цепь длины
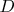 и будем добавлять к вершинам отличным от концевых висячие вершины: к одной -
и будем добавлять к вершинам отличным от концевых висячие вершины: к одной - 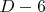 ; к одной - 2; к
; к одной - 2; к 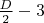 - по одной.
- по одной.Сумма степеней вершин полученного графа составит
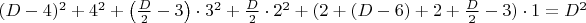 .
Обсуждение
.
ОбсуждениеСуществует много различных способов построения подходящих графов для четных
 . Вариант приведенный в решении предложен Кириллом Веденским и Анатолием Казмерчуком.
. Вариант приведенный в решении предложен Кириллом Веденским и Анатолием Казмерчуком.Еще один универсальный метод предложен Виктором Филимоненковым: к одной из внутренних вершин вершин цепи длины
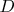 прицепим 2 висячие вершины, а к другой -
прицепим 2 висячие вершины, а к другой - 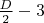 трехвзенных цикла.
трехвзенных цикла.Другие подходы (в том числе и авторский) либо содержат исключения для малых значений
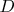 , либо варьируются, например, в зависимости от
, либо варьируются, например, в зависимости от 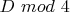 .
. Уже не в первый раз (хотя я и не смог найти в архиве, когда был первый раз) некоторые марафонцы загадочным образом ухитряются найти диаметр графа, не являющегося связным. Насколько я в курсе (а я, полагаю, в курсе), диаметр (как и расстояние, через которое он вводится) определяется только для связного графа.
Награды
За правильное решение задачи ММ146 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Дмитрий Пашуткин, Кирилл Веденский и Андрей Халявин получают по 4 призовых балла. Александр Ларин получает 2 призовых балла.
Эстетическая оценка - 4.6 балла
Разбор задачи ММ146 подготовил Владимир Лецко
Задайте вопрос на блоге о математике
