- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона: 12↓
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
======= 149 ========
ММ149 (8 баллов)
При каком наименьшем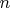 в группе перестановок
в группе перестановок 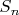 существует подгруппа порядка 253? Привести пример такой подгруппы.
существует подгруппа порядка 253? Привести пример такой подгруппы.
====================
Решение
Приведу решение Андрея Халявина, замечательное своей краткостью.
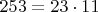 . Поэтому по теореме Силова в подгруппе должен быть элемент порядка 23. Значит,
. Поэтому по теореме Силова в подгруппе должен быть элемент порядка 23. Значит,  .
.
Пусть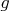 - первообразный корень по модулю 23. Тогда подгруппа группы
- первообразный корень по модулю 23. Тогда подгруппа группы 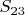 , состоящая из перестановок
, состоящая из перестановок 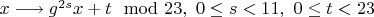 , имеет порядок 253.
, имеет порядок 253.
Ответ: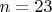 Обсуждение
Обсуждение
Приведу более лобовой (если хотите, более тупой) способ построения требуемой подгруппы группы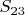 .
.
Возьмем цикл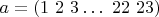 и будем строить перестановку
и будем строить перестановку 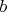 такую, что
такую, что 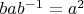 .
.
Заметим, что 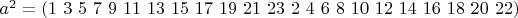 .
.
Пусть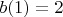 . Тогда при
. Тогда при 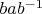 имеем:
имеем:  . Значит,
. Значит, 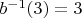 и
и 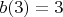 .
.
Тогда . Значит,
. Значит, 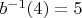 и
и 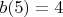 .
.
Тогда . Значит,
. Значит, 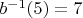 и
и 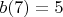 .
.
Тогда . Значит,
. Значит, 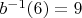 и
и 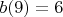 .
.
Продолжая в том же духе, получим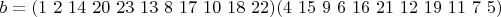 .
.
Непосредственно проверяется, что подгруппа, порожденная и
и 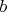 , имеет порядок 253.
, имеет порядок 253.
Пусть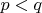 - простые числа. С помощью теоремы Силова легко доказывается, что, если
- простые числа. С помощью теоремы Силова легко доказывается, что, если 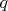 не сравнимо с 1 по модулю
не сравнимо с 1 по модулю 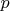 , то группа порядка
, то группа порядка 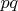 циклическая. Такая группа может быть реализована перестановками множества, состоящего не менее, чем из
циклическая. Такая группа может быть реализована перестановками множества, состоящего не менее, чем из 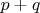 элементов.
элементов.
Если же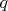 сравнимо с 1 по модулю
сравнимо с 1 по модулю 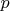 , то обязательно найдется группа порядка
, то обязательно найдется группа порядка 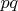 , реализуемая перестановками из
, реализуемая перестановками из 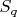 . Подробности можно найти, например, в книжке М.Каргаполов, Ю.Мерзляков. "Основы теории групп"
. Подробности можно найти, например, в книжке М.Каргаполов, Ю.Мерзляков. "Основы теории групп"
Награды
За правильное решение и обобщение задачи ММ149 Алексей Волошин получает 9 призовых баллов. Анатолий Казмерчук, Виктор Филимоненков, Sirion и Андрей Халявин получают по 8 призовых баллов. Сергей Половинкин и Дмитрий Пашуткин (нашедшие нужные подгруппы лишь в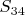 ) получают по 2 призовых балла.
) получают по 2 призовых балла.
Эстетическая оценка - 5 баллов
Разбор задачи ММ149 подготовил Владимир Лецко
-- 23 окт 2011, 11:41 --
=================================
ММ149 (8 баллов)
При каком наименьшем
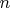 в группе перестановок
в группе перестановок 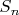 существует подгруппа порядка 253? Привести пример такой подгруппы.
существует подгруппа порядка 253? Привести пример такой подгруппы.====================
Решение
Приведу решение Андрея Халявина, замечательное своей краткостью.
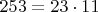 . Поэтому по теореме Силова в подгруппе должен быть элемент порядка 23. Значит,
. Поэтому по теореме Силова в подгруппе должен быть элемент порядка 23. Значит,  .
.Пусть
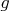 - первообразный корень по модулю 23. Тогда подгруппа группы
- первообразный корень по модулю 23. Тогда подгруппа группы 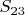 , состоящая из перестановок
, состоящая из перестановок 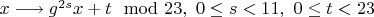 , имеет порядок 253.
, имеет порядок 253.Ответ:
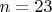 Обсуждение
ОбсуждениеПриведу более лобовой (если хотите, более тупой) способ построения требуемой подгруппы группы
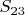 .
.Возьмем цикл
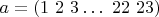 и будем строить перестановку
и будем строить перестановку 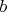 такую, что
такую, что 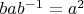 .
.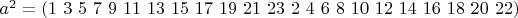 .
.Пусть
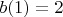 . Тогда при
. Тогда при 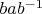 имеем:
имеем:  . Значит,
. Значит, 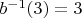 и
и 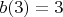 .
.Тогда
 . Значит,
. Значит, 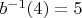 и
и 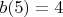 .
.Тогда
 . Значит,
. Значит, 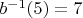 и
и 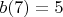 .
.Тогда
 . Значит,
. Значит, 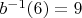 и
и 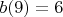 .
.Продолжая в том же духе, получим
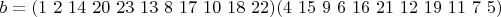 .
.Непосредственно проверяется, что подгруппа, порожденная
 и
и 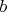 , имеет порядок 253.
, имеет порядок 253. Пусть
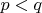 - простые числа. С помощью теоремы Силова легко доказывается, что, если
- простые числа. С помощью теоремы Силова легко доказывается, что, если 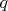 не сравнимо с 1 по модулю
не сравнимо с 1 по модулю 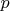 , то группа порядка
, то группа порядка 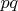 циклическая. Такая группа может быть реализована перестановками множества, состоящего не менее, чем из
циклическая. Такая группа может быть реализована перестановками множества, состоящего не менее, чем из 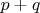 элементов.
элементов.Если же
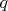 сравнимо с 1 по модулю
сравнимо с 1 по модулю 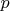 , то обязательно найдется группа порядка
, то обязательно найдется группа порядка 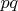 , реализуемая перестановками из
, реализуемая перестановками из 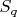 . Подробности можно найти, например, в книжке М.Каргаполов, Ю.Мерзляков. "Основы теории групп"
. Подробности можно найти, например, в книжке М.Каргаполов, Ю.Мерзляков. "Основы теории групп" Награды
За правильное решение и обобщение задачи ММ149 Алексей Волошин получает 9 призовых баллов. Анатолий Казмерчук, Виктор Филимоненков, Sirion и Андрей Халявин получают по 8 призовых баллов. Сергей Половинкин и Дмитрий Пашуткин (нашедшие нужные подгруппы лишь в
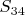 ) получают по 2 призовых балла.
) получают по 2 призовых балла. Эстетическая оценка - 5 баллов
Разбор задачи ММ149 подготовил Владимир Лецко
-- 23 окт 2011, 11:41 --
=================================
Задайте вопрос на блоге о математике
