- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона: 12↓
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
======= 148 ========
ММ148 (8 баллов)
Сколько внутренних диагоналей может иметь n-угольник?
===============
Решение
Приведу решение Виктора Филимоненкова.
Решение: Сначала по индукции докажем, что у любого n-угольника существует по крайней мере n-3 внутренние диагонали.
Для треугольника это утверждение очевидно.
Пусть утверждение выполнено для любого k, меньшего n. Докажем, что тогда оно верно и для n.
Лемма. У любого n-угольника есть хотя бы одна внутренняя диагональ.
Ясно, что у n-угольника есть угол, меньше развернутого. Действительно, проведем прямую, проходящую вне многоугольника, и будем сдвигать ее в сторону многоугольника. Угол при вершине А, которой прямая коснется первой, будет меньше развернутого.
Рассмотрим две соседние с А вершины В и С. Если диагональ ВС внутренняя, то мы доказали лемму. Если ВС не внутренняя, то она пересекает стороны n-угольника, и внутри треугольника АВС есть вершины треугольника. Возьмем луч АВ и начнем его поворачивать к стороне АС. Пусть Д - первая вершина n-угольника, лежащая внутри АВС. Тогда АД - искомая внутренняя диагональ n-угольника.
Вернемся к доказательству базы индукции. Проведем внутреннюю диагональ в n-угольнике. Она разобьет n-угольник на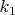 -угольник и
-угольник и 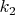 -угольник, где
-угольник, где 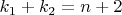 (так как 2 вершины у многоугольников разбиения общие, а остальные вершины n-угольника являются вершинами ровно одного из многоугольников разбиения). Значит, по предположению индукции, всего в n-угольнике, считая диагональ разбиения, не меньше, чем
(так как 2 вершины у многоугольников разбиения общие, а остальные вершины n-угольника являются вершинами ровно одного из многоугольников разбиения). Значит, по предположению индукции, всего в n-угольнике, считая диагональ разбиения, не меньше, чем 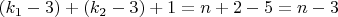 внутренние диагонали.
внутренние диагонали.
Покажем, что многоугольник с таким числом внутренних диагоналей существует.
Действительно, рассмотрим окружность с центром О и точку А вне нее. Проведем из А два касательных отрезка к окружности, Пусть В и С - точки касания. Разобьем дугу ВС на n-3 части, и проведем хорды, стягивающие полученные дужки. В полученном n-угольнике внутренними являются только n-3 диагонали, выходящие из вершины А.

Покажем теперь, что количество внутренних диагоналей может быть и любым, большим чем , вплоть до
, вплоть до 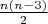 - общего числа диагоналей в n-угольнике. Для этого в многоугольнике, построенном в прошлом абзаце, начнем сдвигать вершины, лежащие между В и С, по лучам, выходящим из А, в сторону дуги окружности ВОС, пока не получим выпуклый многоугольник. Диагонали, выходящие из А, при этом остаются внутренними. Будем добиваться того, чтобы ни в какой момент времени не было одновременно больше одной тройки вершин, лежащих на одной прямой (при необходимости чуть "притормаживая" тот момент, когда или "ускоряя" какие-то вершины). Это гарантирует, что количество внутренних диагоналей не будет меняться более, чем 1. Так как в конце движения таких диагоналей становится n(n-3)/2, а в начале движения (n-3), то в процессе движения возникали многоугольники с любым количеством внутренних диагоналей от между этими двумя числами.
- общего числа диагоналей в n-угольнике. Для этого в многоугольнике, построенном в прошлом абзаце, начнем сдвигать вершины, лежащие между В и С, по лучам, выходящим из А, в сторону дуги окружности ВОС, пока не получим выпуклый многоугольник. Диагонали, выходящие из А, при этом остаются внутренними. Будем добиваться того, чтобы ни в какой момент времени не было одновременно больше одной тройки вершин, лежащих на одной прямой (при необходимости чуть "притормаживая" тот момент, когда или "ускоряя" какие-то вершины). Это гарантирует, что количество внутренних диагоналей не будет меняться более, чем 1. Так как в конце движения таких диагоналей становится n(n-3)/2, а в начале движения (n-3), то в процессе движения возникали многоугольники с любым количеством внутренних диагоналей от между этими двумя числами.
Ответ: любое целое число от до
до 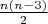 Обсуждение
Обсуждение
Все n-3 диагонали n-угольников, имеющих ровно n-3 внутренних диагонали, конечно не обязаны исходить из одной вершины.
Ниже приведены примеры совсем другого расположения внутренних диагоналей.
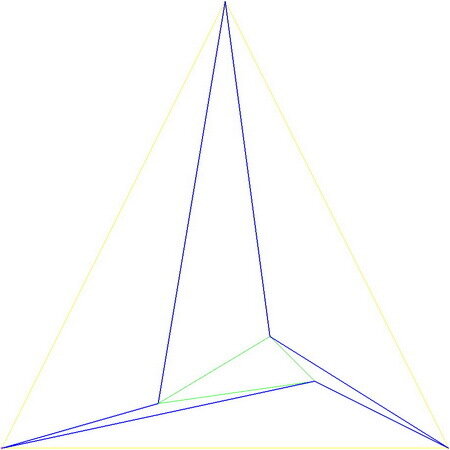
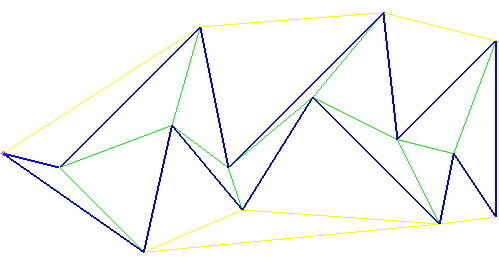
Но одну особенность n-3,n-угольники, имеющие ровно n-3 внутренних диагонали, все же имеют:
Из приведенного в решении доказательства легко выводится такое утверждение: количество внутренних диагоналей n-угольника равно n-3 тогда и только тогда, когда никакие две из них не пересекаются внутри треугольника.
Иными словами, такие многоугольники имеют единственную триангуляцию диагоналями на n-2 треугольника.
При решении данной задачи очень ярко проявились разночтения в понимании разными людьми очевидности в математике.
С моей (безусловно субъективной) точки зрения, наличие и любого многоугольника хотя бы одной внутренней диагонали и, тем более, триангуляции совсем не очевидна. В то же время, достижимость всех промежуточных случаев от до
до 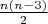 внутренних при некоторой деформации n-угольника, имеющего ровно n-3 внутренних диагонали, в выпуклый, представляется мне вполне очевидной.
внутренних при некоторой деформации n-угольника, имеющего ровно n-3 внутренних диагонали, в выпуклый, представляется мне вполне очевидной.
Некоторые участники марафона наоборот посчитали очевидным наличие триангуляции и все внимание сосредоточили на (гораздо более подробном, чем приведенное) доказательстве достижимости промежуточных случаев.
Были и те, кому было не очевидно ни первое, ни второе. А также те, кому наоборот все было очевидно.
Награды
За правильное решение задачи ММ148 Анатолий Казмерчук, Виктор Филимоненков, Сергей Половинкин и Дмитрий Пашуткин получают по 8 призовых баллов. Алексей Волошин, получает 7, а Александр Ларин - 6 призовых баллов.
Эстетическая оценка - 4.4 балла
Разбор задачи ММ148 подготовил Владимир Лецко
-- 16 окт 2011, 17:56 --
=================================
ММ148 (8 баллов)
Сколько внутренних диагоналей может иметь n-угольник?
===============
Решение
Приведу решение Виктора Филимоненкова.
Решение: Сначала по индукции докажем, что у любого n-угольника существует по крайней мере n-3 внутренние диагонали.
Для треугольника это утверждение очевидно.
Пусть утверждение выполнено для любого k, меньшего n. Докажем, что тогда оно верно и для n.
Лемма. У любого n-угольника есть хотя бы одна внутренняя диагональ.
Ясно, что у n-угольника есть угол, меньше развернутого. Действительно, проведем прямую, проходящую вне многоугольника, и будем сдвигать ее в сторону многоугольника. Угол при вершине А, которой прямая коснется первой, будет меньше развернутого.
Рассмотрим две соседние с А вершины В и С. Если диагональ ВС внутренняя, то мы доказали лемму. Если ВС не внутренняя, то она пересекает стороны n-угольника, и внутри треугольника АВС есть вершины треугольника. Возьмем луч АВ и начнем его поворачивать к стороне АС. Пусть Д - первая вершина n-угольника, лежащая внутри АВС. Тогда АД - искомая внутренняя диагональ n-угольника.
Вернемся к доказательству базы индукции. Проведем внутреннюю диагональ в n-угольнике. Она разобьет n-угольник на
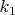 -угольник и
-угольник и 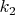 -угольник, где
-угольник, где 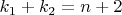 (так как 2 вершины у многоугольников разбиения общие, а остальные вершины n-угольника являются вершинами ровно одного из многоугольников разбиения). Значит, по предположению индукции, всего в n-угольнике, считая диагональ разбиения, не меньше, чем
(так как 2 вершины у многоугольников разбиения общие, а остальные вершины n-угольника являются вершинами ровно одного из многоугольников разбиения). Значит, по предположению индукции, всего в n-угольнике, считая диагональ разбиения, не меньше, чем 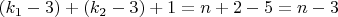 внутренние диагонали.
внутренние диагонали.Покажем, что многоугольник с таким числом внутренних диагоналей существует.
Действительно, рассмотрим окружность с центром О и точку А вне нее. Проведем из А два касательных отрезка к окружности, Пусть В и С - точки касания. Разобьем дугу ВС на n-3 части, и проведем хорды, стягивающие полученные дужки. В полученном n-угольнике внутренними являются только n-3 диагонали, выходящие из вершины А.

Покажем теперь, что количество внутренних диагоналей может быть и любым, большим чем
 , вплоть до
, вплоть до 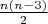 - общего числа диагоналей в n-угольнике. Для этого в многоугольнике, построенном в прошлом абзаце, начнем сдвигать вершины, лежащие между В и С, по лучам, выходящим из А, в сторону дуги окружности ВОС, пока не получим выпуклый многоугольник. Диагонали, выходящие из А, при этом остаются внутренними. Будем добиваться того, чтобы ни в какой момент времени не было одновременно больше одной тройки вершин, лежащих на одной прямой (при необходимости чуть "притормаживая" тот момент, когда или "ускоряя" какие-то вершины). Это гарантирует, что количество внутренних диагоналей не будет меняться более, чем 1. Так как в конце движения таких диагоналей становится n(n-3)/2, а в начале движения (n-3), то в процессе движения возникали многоугольники с любым количеством внутренних диагоналей от между этими двумя числами.
- общего числа диагоналей в n-угольнике. Для этого в многоугольнике, построенном в прошлом абзаце, начнем сдвигать вершины, лежащие между В и С, по лучам, выходящим из А, в сторону дуги окружности ВОС, пока не получим выпуклый многоугольник. Диагонали, выходящие из А, при этом остаются внутренними. Будем добиваться того, чтобы ни в какой момент времени не было одновременно больше одной тройки вершин, лежащих на одной прямой (при необходимости чуть "притормаживая" тот момент, когда или "ускоряя" какие-то вершины). Это гарантирует, что количество внутренних диагоналей не будет меняться более, чем 1. Так как в конце движения таких диагоналей становится n(n-3)/2, а в начале движения (n-3), то в процессе движения возникали многоугольники с любым количеством внутренних диагоналей от между этими двумя числами.Ответ: любое целое число от
 до
до 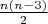 Обсуждение
ОбсуждениеВсе n-3 диагонали n-угольников, имеющих ровно n-3 внутренних диагонали, конечно не обязаны исходить из одной вершины.
Ниже приведены примеры совсем другого расположения внутренних диагоналей.


Но одну особенность n-3,n-угольники, имеющие ровно n-3 внутренних диагонали, все же имеют:
Из приведенного в решении доказательства легко выводится такое утверждение: количество внутренних диагоналей n-угольника равно n-3 тогда и только тогда, когда никакие две из них не пересекаются внутри треугольника.
Иными словами, такие многоугольники имеют единственную триангуляцию диагоналями на n-2 треугольника.
При решении данной задачи очень ярко проявились разночтения в понимании разными людьми очевидности в математике.
С моей (безусловно субъективной) точки зрения, наличие и любого многоугольника хотя бы одной внутренней диагонали и, тем более, триангуляции совсем не очевидна. В то же время, достижимость всех промежуточных случаев от
 до
до 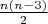 внутренних при некоторой деформации n-угольника, имеющего ровно n-3 внутренних диагонали, в выпуклый, представляется мне вполне очевидной.
внутренних при некоторой деформации n-угольника, имеющего ровно n-3 внутренних диагонали, в выпуклый, представляется мне вполне очевидной.Некоторые участники марафона наоборот посчитали очевидным наличие триангуляции и все внимание сосредоточили на (гораздо более подробном, чем приведенное) доказательстве достижимости промежуточных случаев.
Были и те, кому было не очевидно ни первое, ни второе. А также те, кому наоборот все было очевидно.
Награды
За правильное решение задачи ММ148 Анатолий Казмерчук, Виктор Филимоненков, Сергей Половинкин и Дмитрий Пашуткин получают по 8 призовых баллов. Алексей Волошин, получает 7, а Александр Ларин - 6 призовых баллов.
Эстетическая оценка - 4.4 балла
Разбор задачи ММ148 подготовил Владимир Лецко
-- 16 окт 2011, 17:56 --
=================================
Задайте вопрос на блоге о математике
