- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона: 12↓
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
======= 145 ========
ММ145 (КГ12) (3 балла)
Сколько внешних диагоналей может иметь n-угольгик?
====================
Решение
Пусть между двумя соседними вершинами выпуклой оболочки многоугольника расположено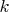 вершин, не входящих в выпуклую оболочку. Тогда соответствующая "впадина" содержит не более
вершин, не входящих в выпуклую оболочку. Тогда соответствующая "впадина" содержит не более 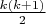 внешних диагоналей.
внешних диагоналей.
Пусть в одной "впадине"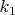 промежуточных вершин, а в другой
промежуточных вершин, а в другой 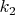 и
и 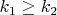 . "Перебрасывая" одну промежуточную вершину из второй впадины в первую, мы увеличим максимально возможное число внешних диагоналей.
. "Перебрасывая" одну промежуточную вершину из второй впадины в первую, мы увеличим максимально возможное число внешних диагоналей.
Поэтому наибольшее число внешних диагоналей достигается, когда "впадина" одна и содержит промежуточных вершины (как минимум три вершины принадлежат выпуклой оболочке) и
промежуточных вершины (как минимум три вершины принадлежат выпуклой оболочке) и 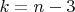 .
.
В случае когда все промежуточные и две смежные им вершины образуют ломаную, "выпуклую в обратную сторону", число внешних диагоналей достигает 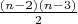 .
.
Среди многочисленных способов обоснования того, что все промежуточные значения от 0 до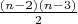 достижимы приведу вариант, предложенный Дмитрием Пашуткиным:
достижимы приведу вариант, предложенный Дмитрием Пашуткиным:

Собственно говоря, все видно из чертежа. Все промежуточные значения можно получить, меняя параметр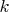 и угол наклона стороны
и угол наклона стороны 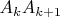 .
Обсуждение
.
Обсуждение
Любопытно, что подавляющее большинство участников Марафона в качестве вспомогательного средства для решения данной задачи использовало решение задачи ММ148 (на мой субъективный взгляд, значительно более трудной).
При этом строгость обоснования вспомогательного утверждения была разной. При оценивании решения ММ148 эта разная строгость нашла бы отражение в призовых баллах (цена ММ148 - 8 баллов). Но ММ145 оценивается всего в 3 балла, а решение ММ148 составляет лишь часть решения ММ145. В такой ситуации разница в строгости обоснования утвеждения про внутренние диагонали на итоговую оценку не повлияла.
Как же теперь поступать при оценивании ММ148 пока не знаю...
Награды
За правильное решение задачи ММ145 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Николай Дерюгин, Дмитрий Пашуткин, Кирилл Веденский и Александр Ларин получают по 3 призовых балла. Андрей Халявин получает 2 призовых балла.
Эстетическая оценка - 4.6 балла
Разбор задачи ММ145 подготовил Владимир Лецко
ММ145 (КГ12) (3 балла)
Сколько внешних диагоналей может иметь n-угольгик?
====================
Решение
Пусть между двумя соседними вершинами выпуклой оболочки многоугольника расположено
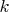 вершин, не входящих в выпуклую оболочку. Тогда соответствующая "впадина" содержит не более
вершин, не входящих в выпуклую оболочку. Тогда соответствующая "впадина" содержит не более 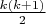 внешних диагоналей.
внешних диагоналей. Пусть в одной "впадине"
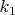 промежуточных вершин, а в другой
промежуточных вершин, а в другой 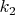 и
и 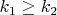 . "Перебрасывая" одну промежуточную вершину из второй впадины в первую, мы увеличим максимально возможное число внешних диагоналей.
. "Перебрасывая" одну промежуточную вершину из второй впадины в первую, мы увеличим максимально возможное число внешних диагоналей.Поэтому наибольшее число внешних диагоналей достигается, когда "впадина" одна и содержит
 промежуточных вершины (как минимум три вершины принадлежат выпуклой оболочке) и
промежуточных вершины (как минимум три вершины принадлежат выпуклой оболочке) и 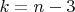 .
.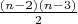 .
.Среди многочисленных способов обоснования того, что все промежуточные значения от 0 до
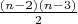 достижимы приведу вариант, предложенный Дмитрием Пашуткиным:
достижимы приведу вариант, предложенный Дмитрием Пашуткиным:
Собственно говоря, все видно из чертежа. Все промежуточные значения можно получить, меняя параметр
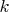 и угол наклона стороны
и угол наклона стороны 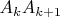 .
Обсуждение
.
ОбсуждениеЛюбопытно, что подавляющее большинство участников Марафона в качестве вспомогательного средства для решения данной задачи использовало решение задачи ММ148 (на мой субъективный взгляд, значительно более трудной).
При этом строгость обоснования вспомогательного утверждения была разной. При оценивании решения ММ148 эта разная строгость нашла бы отражение в призовых баллах (цена ММ148 - 8 баллов). Но ММ145 оценивается всего в 3 балла, а решение ММ148 составляет лишь часть решения ММ145. В такой ситуации разница в строгости обоснования утвеждения про внутренние диагонали на итоговую оценку не повлияла.
Как же теперь поступать при оценивании ММ148 пока не знаю...
Награды
За правильное решение задачи ММ145 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Николай Дерюгин, Дмитрий Пашуткин, Кирилл Веденский и Александр Ларин получают по 3 призовых балла. Андрей Халявин получает 2 призовых балла.
Эстетическая оценка - 4.6 балла
Разбор задачи ММ145 подготовил Владимир Лецко
Задайте вопрос на блоге о математике
