- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона: 12↓
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM (7)→
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир - Часть 2
- Отбор на XVI Всеукраинский турнир - Часть 1
- Далеко, далеко, на лугу пасутся ко...
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
=================================================
ММ144 (5 баллов)
На поле e4 стоит чёрный король. Первый игрок ставит на любую клетку доски, не находящуюся под боем чёрного короля, белых королей (по одному за ход). Второй игрок делает (правильный) ход чёрным королём. Игра заканчивается, когда у чёрного короля не будет ходов. Каково минимальное количество ходов, за которое первый игрок может достичь цели?
=================================================
Решение
Приведём решение Сергея Половинкина.
Пусть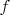 - минимальное количество ходов, за которое первый игрок может достичь цели при некотором заданном положении черного короля.
- минимальное количество ходов, за которое первый игрок может достичь цели при некотором заданном положении черного короля.
На следующих рисунках приведены значения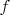 для квадратных досок для всех начальных положений черного короля.
для квадратных досок для всех начальных положений черного короля.



Можно сделать некоторые выводы (за небольшими исключениями):
1. Для угловых клеток -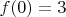
2. Слои клеток на краях доски (без углов), назовем эти слои первыми -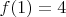
3. Для слоев клеток, соседних с краевыми слоями (пусть это будет второй слой)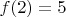
4. Для третьего слоя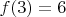
5. Для более дальних слоев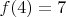 и
и 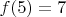 .
.
6. Исключения представляют клетки в 1-ом и 2-ом слоях, расположенные в 3-ем слое относительно другого края (поля с1, с2 или а3, b3).
7. Есть еще и не типовые исключения - на досках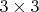 и
и 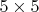
Разберем эти результаты подробнее. Понятно, что на краю доски (особенно в углах) проще запатовать короля черных, поэтому при удалении от края значения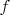 возрастают.
возрастают.
С другой стороны, в некоторых случаях, отсутствие возможности белым "зайти с тыла", ограничивает возможности патования, это объясняет п.6.
Рассмотрим соответствующий пример.
Начальное положение черного короля удобно задать в виде нулевого хода черных, а каждый следующий ход с номером - выставление белого короля и ход черного.
Возьмем доску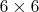 и рассмотрим типовую партию при черном короле на b2:
и рассмотрим типовую партию при черном короле на b2:

0. ... Крb2
1. Крd3
Белые играют естественным образом, черным, чтобы сразу не попасть на край доски (где белые выиграют проще и быстрее) приходится играть
1. ... Крb3

И теперь белые отсекают черных снизу, играя
2. Крb1! Крb4
Черные сделали вынужденный ход, хотя следующий свой ход белые бы сделали на любой ход черных
3. Крb6!
Отсекая черных сверху!

У черных осталось всего 4 клетки, своим 4-м ходом белые уменьшат это количество до двух, а 5-м - запатуют черных.
А на доске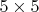 белые лишены возможности "отсечь" черных сверху на 3-ем ходу, именно поэтому при короле на
белые лишены возможности "отсечь" черных сверху на 3-ем ходу, именно поэтому при короле на 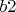 выигрыш белых на досках всех размерностей достигается быстрее, чем на доске
выигрыш белых на досках всех размерностей достигается быстрее, чем на доске 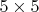 !
!
Там есть еще одна "хитрость", поэтому покажем соответствующую партию.
0. ... Крb2
1. Крd4! Крb3
2. Kpb1 Kpb4
3. Kpb2 Kpa5!

Белые сыграли тоньше на 1-ом ходу, черные делают прекрасный 3-ий ход, два края доски не дают белым возможности выиграть быстрее 6-ти ходов!
Нечто подобное, только попроще, происходит при короле на с1 (а3).
Теперь как выигрывают белые за 6 ходов при короле черных на 3-ей линии.
Пусть черный король стоит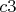 на доске
на доске 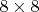 , белые отвечают, например,
, белые отвечают, например, 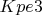

Основной вариант
0. ... Крc3
1. Крe3 Крc4
2. Kpc6 Kpb4
3. Kpb6 Kpb3
4. Kpb1

Как бы теперь ни играли черные, белые патуют их за 2 хода, например:
4. ... Крb4 5. Kpb2 Kpc4 6. Kpa4 или 4. ... Крc4 5. Kpa4 Kpc3 6. Kpc5
или 4. ... Крc4 5. Kpa4 Kpc3 6. Kpc5 
Другие варианты:
1. ... Крc2 2. Kpa2 Kpd1 3. Kpd3 или 1. ... Крb3 2. Kpb1 Kpb4 3. Kpb6 с переходом к основному варианту.
Таким образом можно запатовать короля черных на любом поле 3-ей линии за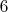 ходов, в том числе и при попадании на "неудобные" поля типа
ходов, в том числе и при попадании на "неудобные" поля типа 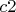 и
и 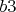 .
.
Теперь понятно, как проще всего выиграть за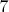 ходов в искомой позиции. При короле на
ходов в искомой позиции. При короле на 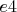 можно пойти 1. Крc5 и теперь черный король имеет неутешительный выбор - или пойти на 3-ю линию (где мы выигрываем за 6 ходов как уже показано) или сделать ход 1. ... Крe5 , что еще быстрее проигрывает после 2. Крg5 с простыми вариантами.
можно пойти 1. Крc5 и теперь черный король имеет неутешительный выбор - или пойти на 3-ю линию (где мы выигрываем за 6 ходов как уже показано) или сделать ход 1. ... Крe5 , что еще быстрее проигрывает после 2. Крg5 с простыми вариантами.
На самом деле к выигрышу белых в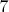 ходов ведет множество продолжений, вот они
ходов ведет множество продолжений, вот они

На этом рисунке показано - за сколько ходов выигрывают белые при соответствующем первом ходе короля. Обсуждение=================================================
Рассмотрим доски большего размера.
Могут возникнуть 2 гипотезы - 7 ходов хватит для патования короля на доске любого размера или количество ходов будет и дальше расти. На самом деле число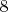 впервые появляется на доске
впервые появляется на доске 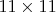

Но дальнейшего роста уже не происходит, за 8 ходов можно запатовать черного короля на бесконечной доске.
Посмотрим, как это происходит на доске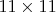 , черный король расположен на
, черный король расположен на 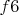 , белые играют королем на
, белые играют королем на 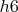 . Теперь черные должны играть очень точно, сделать серию единственных ходов, чтобы не проиграть быстрее 8 ходов :
. Теперь черные должны играть очень точно, сделать серию единственных ходов, чтобы не проиграть быстрее 8 ходов :

С учетом симметрии у черных 3 возможных хода -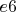 ,
, 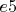 (
(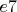 ) и
) и 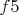 (
(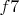 ). Но в тогда в случае 0. ... Крf6 1. Kph6 Kpe6 2. Kpc6 и белые выигрывают в 7 ходов по уже показанным образцам, также достаточно 7 ходов и после 0. ... Крf6 1. Kph6 Kpf5 2. Kpd4 .
). Но в тогда в случае 0. ... Крf6 1. Kph6 Kpe6 2. Kpc6 и белые выигрывают в 7 ходов по уже показанным образцам, также достаточно 7 ходов и после 0. ... Крf6 1. Kph6 Kpf5 2. Kpd4 .
Таким образом, черные обязаны играть 0. ... Крf6 1. Kph6 Kpe5! . Восклицательный знак означает единственность хода.
Далее возможны следующие варианты
2. Kpd3 Kpd6!
2. Kpc4 Kpd6! 3. Kpb7 Kpe7!
2. Kpc4 Kpd6! 3. Kpe5 Kpc7!
И только в случае этих единственных ходов белым потребуется 8 ходов.
Но самый интересный такой вариант
2. Kpc5 Kpf4!
Теперь на 3. Kpf2 у черных есть 2 допустимых хода - на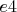 и
и 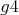 , поэтому сильнее
, поэтому сильнее
3. Kpg2 Kpe4! , а на 4. Kpe2 уже любой из 3-х возможных ходов черных ведет к выигрышу на 8-ом ходу. Но при этом белые не пускают черного короля к краю доски, т.е. запатовывают его в центре. Белые могли поставить больше проблем на 4-ом ходу, сходив на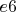 или
или 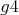 , тогда у черных было бы по 2 допустимых хода.
, тогда у черных было бы по 2 допустимых хода.
Поскольку в этой партии ни одна сторона не пользовалась краями доски, то можно к 7 приведенным выше пунктам, добавить 8-ой: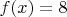 при
при 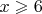 .
.
Награды=================================================
За правильное решение задачи и развитие темы Сергей Половинкин получает 5+2=7 призовых баллов.
Дмитрий Пашуткин и Анатолий Казмерчук получают 4 балла. Александр Ларин получает 3 балла.
Эстетическая оценка задачи: 5
ММ144 (5 баллов)
На поле e4 стоит чёрный король. Первый игрок ставит на любую клетку доски, не находящуюся под боем чёрного короля, белых королей (по одному за ход). Второй игрок делает (правильный) ход чёрным королём. Игра заканчивается, когда у чёрного короля не будет ходов. Каково минимальное количество ходов, за которое первый игрок может достичь цели?
=================================================
Решение
Приведём решение Сергея Половинкина.
Пусть
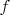 - минимальное количество ходов, за которое первый игрок может достичь цели при некотором заданном положении черного короля.
- минимальное количество ходов, за которое первый игрок может достичь цели при некотором заданном положении черного короля.На следующих рисунках приведены значения
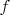 для квадратных досок для всех начальных положений черного короля.
для квадратных досок для всех начальных положений черного короля.


Можно сделать некоторые выводы (за небольшими исключениями):
1. Для угловых клеток -
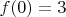
2. Слои клеток на краях доски (без углов), назовем эти слои первыми -
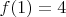
3. Для слоев клеток, соседних с краевыми слоями (пусть это будет второй слой)
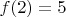
4. Для третьего слоя
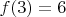
5. Для более дальних слоев
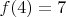 и
и 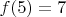 .
.6. Исключения представляют клетки в 1-ом и 2-ом слоях, расположенные в 3-ем слое относительно другого края (поля с1, с2 или а3, b3).
7. Есть еще и не типовые исключения - на досках
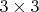 и
и 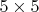
Разберем эти результаты подробнее. Понятно, что на краю доски (особенно в углах) проще запатовать короля черных, поэтому при удалении от края значения
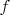 возрастают.
возрастают. С другой стороны, в некоторых случаях, отсутствие возможности белым "зайти с тыла", ограничивает возможности патования, это объясняет п.6.
Рассмотрим соответствующий пример.
Начальное положение черного короля удобно задать в виде нулевого хода черных, а каждый следующий ход с номером - выставление белого короля и ход черного.
Возьмем доску
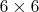 и рассмотрим типовую партию при черном короле на b2:
и рассмотрим типовую партию при черном короле на b2:
0. ... Крb2
1. Крd3
Белые играют естественным образом, черным, чтобы сразу не попасть на край доски (где белые выиграют проще и быстрее) приходится играть
1. ... Крb3

И теперь белые отсекают черных снизу, играя
2. Крb1! Крb4
3. Крb6!
Отсекая черных сверху!

У черных осталось всего 4 клетки, своим 4-м ходом белые уменьшат это количество до двух, а 5-м - запатуют черных.
А на доске
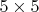 белые лишены возможности "отсечь" черных сверху на 3-ем ходу, именно поэтому при короле на
белые лишены возможности "отсечь" черных сверху на 3-ем ходу, именно поэтому при короле на 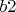 выигрыш белых на досках всех размерностей достигается быстрее, чем на доске
выигрыш белых на досках всех размерностей достигается быстрее, чем на доске 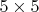 !
!Там есть еще одна "хитрость", поэтому покажем соответствующую партию.
0. ... Крb2
1. Крd4! Крb3
2. Kpb1 Kpb4
3. Kpb2 Kpa5!

Белые сыграли тоньше на 1-ом ходу, черные делают прекрасный 3-ий ход, два края доски не дают белым возможности выиграть быстрее 6-ти ходов!
Нечто подобное, только попроще, происходит при короле на с1 (а3).
Теперь как выигрывают белые за 6 ходов при короле черных на 3-ей линии.
Пусть черный король стоит
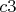 на доске
на доске 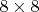 , белые отвечают, например,
, белые отвечают, например, 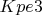

Основной вариант
0. ... Крc3
1. Крe3 Крc4
2. Kpc6 Kpb4
3. Kpb6 Kpb3
4. Kpb1

Как бы теперь ни играли черные, белые патуют их за 2 хода, например:
4. ... Крb4 5. Kpb2 Kpc4 6. Kpa4
 или 4. ... Крc4 5. Kpa4 Kpc3 6. Kpc5
или 4. ... Крc4 5. Kpa4 Kpc3 6. Kpc5 
Другие варианты:
1. ... Крc2 2. Kpa2 Kpd1 3. Kpd3 или 1. ... Крb3 2. Kpb1 Kpb4 3. Kpb6 с переходом к основному варианту.
Таким образом можно запатовать короля черных на любом поле 3-ей линии за
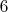 ходов, в том числе и при попадании на "неудобные" поля типа
ходов, в том числе и при попадании на "неудобные" поля типа 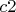 и
и 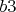 .
.Теперь понятно, как проще всего выиграть за
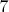 ходов в искомой позиции. При короле на
ходов в искомой позиции. При короле на 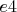 можно пойти 1. Крc5 и теперь черный король имеет неутешительный выбор - или пойти на 3-ю линию (где мы выигрываем за 6 ходов как уже показано) или сделать ход 1. ... Крe5 , что еще быстрее проигрывает после 2. Крg5 с простыми вариантами.
можно пойти 1. Крc5 и теперь черный король имеет неутешительный выбор - или пойти на 3-ю линию (где мы выигрываем за 6 ходов как уже показано) или сделать ход 1. ... Крe5 , что еще быстрее проигрывает после 2. Крg5 с простыми вариантами.На самом деле к выигрышу белых в
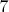 ходов ведет множество продолжений, вот они
ходов ведет множество продолжений, вот они
На этом рисунке показано - за сколько ходов выигрывают белые при соответствующем первом ходе короля. Обсуждение=================================================
Рассмотрим доски большего размера.
Могут возникнуть 2 гипотезы - 7 ходов хватит для патования короля на доске любого размера или количество ходов будет и дальше расти. На самом деле число
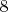 впервые появляется на доске
впервые появляется на доске 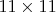

Но дальнейшего роста уже не происходит, за 8 ходов можно запатовать черного короля на бесконечной доске.
Посмотрим, как это происходит на доске
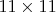 , черный король расположен на
, черный король расположен на 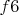 , белые играют королем на
, белые играют королем на 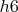 . Теперь черные должны играть очень точно, сделать серию единственных ходов, чтобы не проиграть быстрее 8 ходов :
. Теперь черные должны играть очень точно, сделать серию единственных ходов, чтобы не проиграть быстрее 8 ходов :
С учетом симметрии у черных 3 возможных хода -
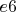 ,
, 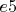 (
(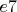 ) и
) и 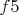 (
(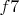 ). Но в тогда в случае 0. ... Крf6 1. Kph6 Kpe6 2. Kpc6 и белые выигрывают в 7 ходов по уже показанным образцам, также достаточно 7 ходов и после 0. ... Крf6 1. Kph6 Kpf5 2. Kpd4 .
). Но в тогда в случае 0. ... Крf6 1. Kph6 Kpe6 2. Kpc6 и белые выигрывают в 7 ходов по уже показанным образцам, также достаточно 7 ходов и после 0. ... Крf6 1. Kph6 Kpf5 2. Kpd4 . Таким образом, черные обязаны играть 0. ... Крf6 1. Kph6 Kpe5! . Восклицательный знак означает единственность хода.
Далее возможны следующие варианты
2. Kpd3 Kpd6!
2. Kpc4 Kpd6! 3. Kpb7 Kpe7!
2. Kpc4 Kpd6! 3. Kpe5 Kpc7!
И только в случае этих единственных ходов белым потребуется 8 ходов.
Но самый интересный такой вариант
2. Kpc5 Kpf4!
Теперь на 3. Kpf2 у черных есть 2 допустимых хода - на
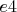 и
и 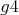 , поэтому сильнее
, поэтому сильнее 3. Kpg2 Kpe4! , а на 4. Kpe2 уже любой из 3-х возможных ходов черных ведет к выигрышу на 8-ом ходу. Но при этом белые не пускают черного короля к краю доски, т.е. запатовывают его в центре. Белые могли поставить больше проблем на 4-ом ходу, сходив на
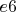 или
или 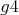 , тогда у черных было бы по 2 допустимых хода.
, тогда у черных было бы по 2 допустимых хода.Поскольку в этой партии ни одна сторона не пользовалась краями доски, то можно к 7 приведенным выше пунктам, добавить 8-ой:
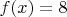 при
при 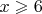 .
.Награды=================================================
За правильное решение задачи и развитие темы Сергей Половинкин получает 5+2=7 призовых баллов.
Дмитрий Пашуткин и Анатолий Казмерчук получают 4 балла. Александр Ларин получает 3 балла.
Эстетическая оценка задачи: 5
Задайте вопрос на блоге о математике
