Решения задач пробного тестирования (ЗНО) по математике 2010 года. Задания 35-36

Задача 35
Тема Уравнения с параметрами. Модули.
Условие: Найдите наибольшее значение параметра а, при котором уравнение имеет ровно 4 корня. Если такого значения не существует, в ответ запишите число 100.

Решение
Построим график функции и рассмотрим, когда он будет иметь ровно 4 точки пересечения с прямой у=а.



Видим, что при a<0 точек пересечения не будет, при a=0 их будет две, затем – четыре, при a=5 точек пересечения будет 6, и при некотором значении a их снова станет четыре. Найти это значение легко, если вспомнить, что данный график был получен из параболы отражением от оси ОY и сгибанием через ось ОХ. И координата вершины параболы перейдёт именно в искомое значение параметра а.





Значит

Ответ: 6,25

Задача 36
Тема Стереометрия.
Условие: В правильную четырёхугольную пирамиду вписана сфера площадью см³. Боковая грань пирамиды наклонена к плоскости её основания под углом 60^o. Найдите объём пирамиды (в см³)

Решение


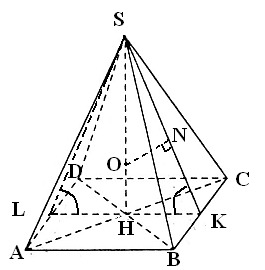
Рассмотрим сечение пирамиды плоскостью SLK, где L и K – середины сторон AD и BC соответственно.



Т.к. в треугольнике SKL углы при основании равны 60 градусов, то он равносторонний. Значит H=3R, , где R=ON=OH – радиус сферы, Н=SH – высота пирамиды, а=KL=AB – сторона основания пирамиды.

Из уравнения
 
находим
 

Тогда


Поскольку площадь сферы выражается по формуле

, то R=3 см и искомый объём равен 324 см³

Ответ: 324

<Назад | Обсудить решения задач в блоге ЗНО 2010 по математике